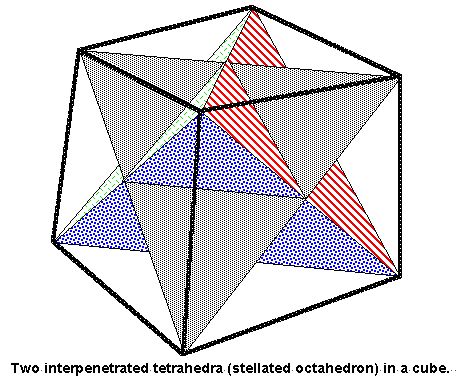
Figure 1. Interpenetrated tetrahedra enclose an octahedron at their core and are surrounded by an external cube.
HTML version of: Longstaff J. S. (2002). Choreutic Tetrahedra. Movement News, 27 (1), 10-12.
A fundamental of choreutic practice includes the use of polyhedra for visualising “kinespheric ‘scaffolding’” providing reference grids or networks for mapping the body’s spatial paths and poses (Laban, 1966, p. 68). The icosahedron is the most common though it is well known that a variety of other polyhedra were also used (Laban, 1966, pp. 104, 116, 121; 1984; Ullmann, 1966, p. 202) and these appear to offer possibilities for the continuing development of space harmony. The purpose of this article is to submit some general thoughts on types of tetrahedral tensions.
 Figure 1. Interpenetrated tetrahedra enclose an octahedron at their core and are surrounded by an external cube. |
The geometry is well known, any tetrahedron having 4 vertices (points), 4 triangle surfaces, and 6 edges. When an octahedron is stellated it creates two interpenetrating tetrahedra around its exterior, while a cube can also be drawn around the 8 verticies of these two tetrahedra (Fig. 1).
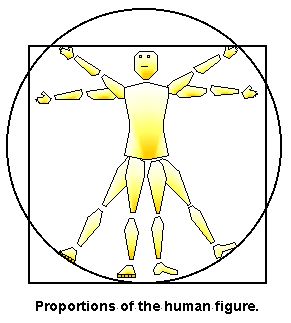 Figure 2. Body representation in frontal plane, in the style of Leonardo Da Vinci (Heydenreich, 1928, p. 110) |
Tetrahedra have traditionally been considered in choreutics as a type of basic or elemental net. In Laban’s (1966) analysis “almost all positions of the body can be reduced or related to a tetrahedral form” (p. 20) and even in “many-directional movements a tetrahedral kernel can, nevertheless, be recognised as the simplest expression of the whole tension” (p. 21).
This elemental conception of the tetrahedron may be linked to the transformation of the frontal planar net into the tetrahedral net whenever the body twists. Frequently the frontal plane of the body is envisaged as a flat surface, one of the most famous examples being Leonardo Da Vinci’s “sketch showing the proportions of the human figure” (Fig. 2) (Heydenreich, 1928, p. 110), and the “grid of proportions” by Le Corbusier (1980, pp. 37-58) (Fig. 3). Laban (1966, pp. 18-21) begins with similar planar conceptions of body space where the two arms and two legs each move into one of the four corners of a plane. From this starting place the body creates “plastic variations of the flat quadrangle” when the arms and legs move out of the flat plane and into a more volume-sculpting tetrahedral form (Fig. 4).
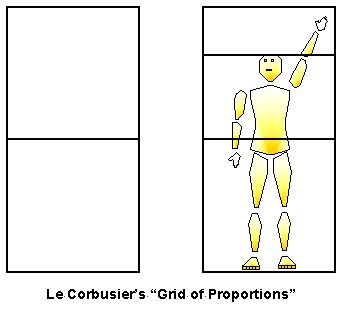 Figure 3. Body representation in frontal plane, in the style of Le Corbusier. |
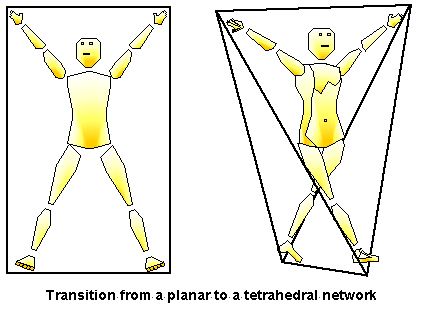 Figure 4. Rudolf Laban described a transition from a plane into a polyhedral network or “kinesphere”. |
This upper/lower contralateral twisting is a typical “tetrahedral tension” which is often seen in leaps (Fig. 5) (Bartenieff & Lewis, 1980, pp. 97-98) or in a smaller kinesphere within the torso during walking and more subtle shaping movements (Laban, 1984, pp. 18, 30-31). As with all polyhedral scaffoldings, they can be ‘sized’, or ‘scaled’ and thus applied to spatial organisation ranging from a global level to more detailed local level. An entire series of bending and flexing tetrahedra can be seen operating at different levels of detail within the body, stacked on top of each other, interpenetrating, and with local tetrahedra encompassed by more global tetrahedra.
By scaling the tetrahedron to different grades of detail, this type of tetrahedron oriented on-edge can be observed in the slight oppositional twist during walking (tetrahedral vertices at 2 hips & 2 shoulders) and at a more local level in the lower body during ballet 4th or 5th position with the vertices at foot, foot, hip, & hip. In this case there is a sensation of the line of the hips twisting against the line between the two feet. When going to relevé, an even smaller tetrahedron can be perceived between the two feet. The 4 tetrahedral vertices being ball & heel of right foot, and ball & heel of left foot.
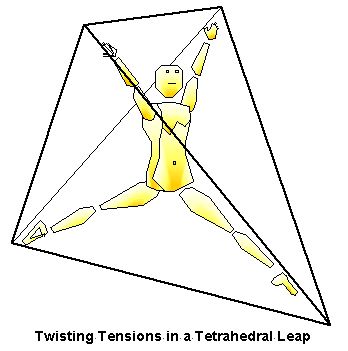 Figure 3. Tetrahedron oriented on-edge as in walking or leaping. |
Other examples can be seen anytime that one line or axis rotates or twists against another line, as in the rotation of the hand (radiocarpal axis) against the shoulder (sagittal axis). Within this whole-arm tetrahedra would be two smaller tetrahedra joined at a common edge (radiohumeral axis). The upper-arm tetrahedron is between the elbow’s axis which rotates against the shoulder sagittal axis. The lower-arm is much more obviously structured, with the radius & ulna being two tetrahedral edges themselves which join the radiohumeral axis (elbow) to the radiocarpal axis (wrist) which twist against each other. This lower-arm tetrahedron can be slightly enlarged if it includes the hand, in this case a line across the hand between thumb and little finger twists against the radiohumeral axis.
This same analysis can be continued to finer levels of detail. Vertebrae function within the spinal column as a tensegrity mast of stacked tetrahedra (Robbie, 1977). And of course the tetrahedral theme can also be finally taken to the micro-level as occurring in the structure of molecules and atoms.
Indeed, in choreutics the tetrahedron has been envisaged as a whole-body spatial form, but also as a much smaller, more detailed component building blocks within other more complex spatial constructions (Laban, 1966, p. 121; 1984, pp. 18, 22, 33). If there is a concept of a fundamental ‘space-flow’ it might be the gradual fluctuation between tetrahedra during the plastic growing and shrinking accompanying breathing. The tetrahedron can be conceived as the four vertices at the two hips and two shoulders which continually shift around each other with a quality of elasticity characteristic of twisting the tetrahedra first one way, and then the other. This tetrahedral space-flow occurs at a local level within all other choreutic forms.
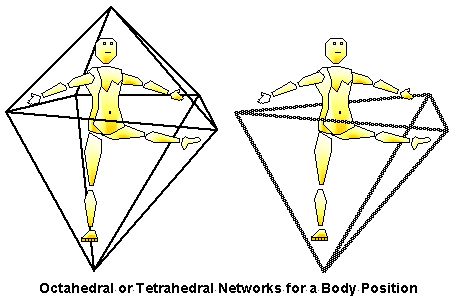 Figure 6. Tetrahedral networds can be found as lower-order nets within other more complex polyhedra. |
A slight variation can be made to this first type of ‘twisting tetrahedron’ to create what might be more of a core-distal pattern. Here the 3 vertices of the tetrahedron consist of three limbs organised around a core with the 4th vertex as the standing leg. This tetrahedron stands on a single point (some examples in Laban, 1984, p. 30) and so may be identical to spatial “chords” where three limbs move into a triangle of mutually counterbalancing orientations while standing on a fourth limb (Bartenieff & Lewis, 1980, pp. 116-117). In cases where three limbs create a chord, there is typically a fourth limb which completes the tetrahedron. This is identical to Laban’s (1966, p. 21) discussion of identifying the “plastic pose” within “four directions”.
A spatial chord might be perceived according to different polyhedra depending on how these scaffolding are sized. While there may be fine distinctions in the physical performance of the chord in Figure 6 which would make it perceived as either octahedral versus tetrahedral, it can also be seen that the general body position can fit into either type of network.
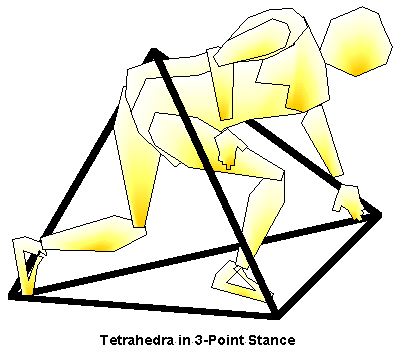 Figure 7. Tetrahedron oriented on-surface such as in a 3-point stance. |
Another type of on-point tetrahedron can be observed at a local level in lower-body articulations. During plié in 1st position the tetrahedron can be seen extending and compressing, standing on the 1st vertex between the heels of the two feet, with the other 3 tetrahedral vertices at knee, knee, and pelvis. This same tetrahedral tension structure can be observed in any plié, with one tetrahedral vertex at ‘place’, where the line-of-gravity touches the floor.
A different tetrahedral form stands on three points, or this might be thought of as being supported on one of the tetrahedron’s triangle surfaces. One example is the common ‘3–point stance’ used in sports (Fig. 7) where the 3 surface points are leg, leg, arm, with the 4th tetrahedral point being the pelvis. In this case the position is stable since it has a wide 3-point support, while the gravity is also readily mobile since it is held high (potential energy).
Another example is the type of ‘sitting’ posture used in meditation or sitting cross-legged (Fig. 8). In this case the 3 surface points are the knee, knee, & pelvis, with the 4th tetrahedral point being the head. Or another slightly smaller tetrahedron might be perceived when the 4th point is the sternum. This same on-surface tetrahedron occurs when the legs are straight, as when dancers sit in ‘2nd position on the floor’.
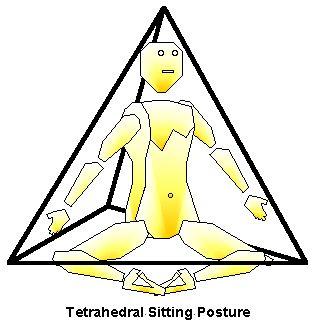 Figure 8. Tetrahedron oriented on-surface in sitting posture. |
At a more local level an on-surface tetrahedron can be seen in the distribution of weight through the foot. The 3 surface points being the two ‘balls of the foot’ and the heel, with the 4th tetrahedral point at the ankle joint (talus). This small tetrahedron can be felt to flex and bend according to how the weight is distributed through the foot. The same tetrahedron can be enlarged to the entire leg if the 4th vertex is taken as the hip.
This review is intended to widen the conception of how tetrahedra might be applied to movement analysis. Hopefully this brief exploration highlights the variety of body-spatial-forms which might be considered to be ‘tetrahedral’.
Bartenieff, I., & Lewis, D. (1980). Body Movement; Coping with the Environment. New York: Gordon and Breach.
Heydenreich, L. H. (1928). Leonardo Da Vinci; Vol. II: plates. New York: MacMillan. (First English edition 1954.)
Laban, R. (1966 [1939]). Choreutics (Annotated and edited by L. Ullmann). London: MacDonald and Evans. (Published in U.S.A. as The Language of Movement: A Guide Book to Choreutics. Boston: Plays.)
Laban, R. (1984). A Vision of Dynamic Space (Compiled by L. Ullmann). London: Falmer Press.
Le Corbusier [Jeanneret-Gris, C. E.] (1980). Modulor I and II. Cambridge: Harvard University Press. (The Modular first published 1954; Modulor II first published 1958.)
Longstaff, J. S. (1996). Cognitive structures of kinesthetic space; Reevaluating Rudolf Laban’s choreutics in the context of spatial cognition and motor control. Ph.D. Thesis. London: City University, Laban Centre.
Robbie, D. L. (1977). Tensional forces in the human body. Orthopaedic Review. VI (11, Nov.): 45–48.
Ullmann, L. (1966). Rudiments of space-movement. In R. Laban, Choreutics (annotated and edited by L. Ullmann) (pp. 138-210). London: MacDonald & Evans.