Figure 1. Examples of planar kinespheric networks.
Summary. -- The choreutic conception of kinesthetic-motor space originally proposed by Rudolf Laban is given psychological validation through comparisons with similar conceptual models in spatial cognition and motor control research. Highly differentiated systems of reference are distinguished. Spatial paths are mentally represented as a series of locations linked into polygonal trajectories. Map-like images of the ‘kinesphere’ are structured with polyhedral networks. A fundamental practice consists of transforming spatial information with various operations (rotation, reflection, sizing, etc.). Loci are linked into spatial ‘scales’ which provide symmetrical solutions to geometric puzzles such as the traveling salesman problem and those devised by Hamilton (Icosian game) and Euler (Koenigsberg bridge problem). In the body these are considered to be prototypes for spatial paths used during adjustments of dynamic equilibrium. The choreutic conception of polyhedral body space is especially similar to the trajectory formation model. The choreutic principal of topological forms deflecting across various kinespheric nets is analogous to N. Bernstein’s description of the “net of the motor field . . . as oscillating like a cobweb in the wind”. These commonalities indicate that further critical reviews of “choreutic laws” might be valuable in suggesting conceptual models and analytical tools for movement study in cognitive science.
Objective analysis and documentation of body movement attributes are critical for distinguishing their role in all areas of human activity. The inadequacy of current psychological concepts becomes evident when attempts are made to analyse body movements in detail (Morasso, 1983b, p. 187; Golani, 1986) or to compile a lexicon of “motor knowledge” or “motor language” (Camurri, Morasso, Tagliasco & Zaccaria, 1986, pp. 104, 116-124). Codification of movement vocabulary, free from any particular style, is necessary for the development of the subfield of psychology concerned with human movement (Whiting, 1986, pp. 116, 124).
One approach to movement study originated by Rudolf Laban (1879-1958) includes major categories of “Labanotation”, “effort”, and “choreutics” (Maletic, 1987). The movement notation system of “Labanotation” or “kinetography Laban” (Preston-Dunlop, 1969; Hutchinson, 1970; Laban, 1975; Knust, 1979), used for the notation of vast numbers of dance works, has been identified as the most stylistic-free method (Hutchinson–Guest, 1989). Categories of movement dynamics or “effort” are reliably observed across independent raters (Davis, 1987) and have been applied in industry (Laban & Lawrence, 1947), Jungian influenced assessment of personality (North, 1972; Hill, 1996), studies of personal motivation and decision making style (Lamb, 1965; Moore, 1982, Winter, Widell, Truitt, & George-Falvy, 1989), theatrical movement (Laban, 1980), and in social and cultural studies (Lomax, Bartenieff & Paulay, 1968; Bartenieff & Lewis, 1980).
“Choreutics” or “space harmony” is a system for conceptualising the spatial forms which can be created with body movements and positions (Laban, 1926; 1966; 1984; Ullmann, 1966; 1971; Dell, 1972; Preston-Dunlop, 1981; 1984). Compared to Labanotation and effort, choreutics has remained largely under-developed though occasionally a few of its features have been applied to dance technique (Bodmer, 1979; Loman, 1987; Winearls, 1990; Lepczyk, 1992), choreography (Sulcas, 1995; Forsythe, 1999), and aerobics (Brody, 1995). Choreutics can also provide a framework for generating and organising stimuli in experimental research (Longstaff, 1996; 1998). However, the underlying “choreutic laws” (Laban, 1966, p. 26) or the “binding laws of harmony” (Ullmann, 1971, p. 1) are not formally organized but remain dispersed in the literature. Because of this lack of critical analyses the validity of choreutics as a method for comprehending spatial attributes of body movements has not been evaluated.
Part of the reason for this lack of a critical reevaluation of choreutics may be the metaphysical associations with the polyhedra which are used for kinespheric maps and the tendency for choreutic writings to contain large doses of esoteric philosophy about the role of movement in the universe (Laban 1966, pp. 54, 91, 100, 114, 124). These mystic associations probably developed through Laban’s involvement in Rosicrucian Freemasonry (Green, 1986; Preston-Dunlop, 1998) and have led choreutics to be ridiculed on philosophical grounds (Langer, 1953, p. 186) while overlooking any serious consideration of its relevance to spatial cognition, kinesiology and movement control.
This research addresses the question of whether choreutic concepts of kinesthetic-motor space have psychological validity. Here, choreutics is reevaluated within the context of spatial cognition and motor control and many similarities are identified between choreutic concepts and psychological models of spatial learning, memory and recall. Dispersed reports throughout the choreutic literature reveal several cognitive structures, including systems of reference, locations linked into polygonal representations of spatial trajectories, map–like mental images of space, the practice of generating spatial transformations, and the principal of deflections (oscillations) across kinespheric nets.
Systems of Reference
Spatial information (eg. directions) must be known relative to a system of reference or its meaning may not be clear. For example, ‘forward’ might be considered relative to the anterior/posterior axis of the body, or it might be considered relative to the front of a room (‘come forward’), etc. The general distinction of reference systems as egocentric or exocentric is identified in choreutics and cognitive studies. In egocentric reference systems (subject-relative, body-based, personal frame, viewer centred) spatial information is interpreted according to the subject’s body (‘forward’ depends on pelvis, torso or head orientation). Exocentric reference systems (object-relative, gravity-based, environmental frame, allocentric) interpret spatial information according to features in the environment (‘upward’ depends on gravity and the orientation of the visual environment).
Reference systems play crucial roles in many contexts. Fine differentiation of body centred references is necessary for descriptions of kinesiology and motor planning (Saltzman, 1979; Paillard, 1987). Experimental research demonstrates how distinguishing and translating between egocentric and exocentric reference is critical for perception and memory of objects (Rock, 1973; Hardwick, McIntyre & Pick, 1976; Marr, 1980; Hinton & Parsons, 1981; Humphreys, 1983) and also of body movements and positions (Rieser & Pick, 1976; Stelmach & Larish, 1980; Larish & Stelmach, 1982). Particular reference systems used across modes, in both verbal descriptions of space and also in non-verbal spatial tasks, can be characteristic of cultural identity (Levinson, 1996).
A multitude of variations on the ‘rod and frame task’ indicate the continual interrelation between egocentric and exocentric referencing. Typically, perceptions of whether an object is ‘vertical’ will be variable depending on the subject’s orientation, the state of their motor system (egocentric effects), and on the orientation of the environment (exocentric effects) (Witkin, Dyk, Faterson, Goodenough & Karp, 1962; McFarland, Werner & Wapner, 1962; Sigman, Goodenough & Flannagan, 1979). Similar effects occur in the context of evoking the tonic neck reflex (Hellebrandt, Schade & Carns, 1962). Consistent differences between subjects led to a distinction between “field-dependent” and “field-independent” perceptual styles (degree of perceptual dependency on the exocentric field) which are correlated with personality characteristics of sociality (exocentric) and bodily awareness (egocentric) (Witkin et al., 1962; Souder, 1972).
A variety of reference systems (likened to musical key signatures) have been distinguished in choreutics and Labanotation (Preston-Dunlop, 1969, p. 136; 1984, pp. 9-12; Hutchinson, 1970, pp. 105-106, 414-433; Knust, 1979, figs. 258b,d,f, 308e, 854b, 859a). The “constant cross” uses a Cartesian (x, y, x) cross of directions oriented relative to a room (or another environment or frame) so that ‘forward’ is toward the front of the room and ‘up’ is with gravity. In “fixed points” referencing any locus can be designated (arbitrarily or not) as representing any spatial direction. A “line of travel” reference system is used when directions are conceived relative to the line of motion (eg. ‘forward’ in ballroom dance is the direction which the couple is moving). The “standard cross” describes the most typical reference system adopted (default value) in which ‘vertical’ is relative to gravity with ‘lateral’ and ‘sagittal’ directions relative to the body. The “body cross” refers to a Cartesian cross oriented relative to the body with its origin centred in any place (hand, pelvis, head, any skeletal joint) so that each body part could function according to its own reference system (Laban, 1926, pp. 72–73; 1966, pp. 11-18; Lamb, 1965, p. 52; Hutchinson, 1970, pp. 32, 229, 307-310; Bodmer, 1974, p. 28; 1979, pp.3-7; Bartenieff & Lewis, 1980, pp. 25-28).
Loci in Polygonal Representations of Spatial Trajectories
Spatial location information plays a primary role in all of cognition. If a person learns the identity of a word or object, then its location is also typically remembered even without any intention by the learner to do so (Mandler, Seegmiller, & Day, 1977; Pezdek, Roman, & Sobolik, 1986) . Memory characteristics function in parallel for separate locations. Words and pictures are learned better when they are presented in separate locations whereas interference occurs when all items are presented in the same location (Crowder, 1978; Broadbent & Broadbent, 1981; Rothkopf, Fisher, & Billington, 1982). A long history of mnemonic strategies have been based on associating each item to be learned with a separate spatial location (Yates, 1966; Bower, 1970; Paivio, 1979, pp. 153-175).
Primacy of location information is also exhibited in movement recall. In limb positioning tasks recalling a location with the body is typically more accurate than recalling a distance moved (Russell, 1976; Kelso, 1977; Roy, 1977; Wallace, 1977; Stelmach & Larish, 1980). Similarly, elemental locations are evident in “equifinality” of motor behaviour where body linkages automatically correct errors and achieve a final end-position regardless of unexpected variables such as encountering an obstacle or unexpected limb perturbations. According to the mass-spring model of motor control equifinality occurs because movement is generated by resetting an “equilibrium point” between tensions of agonist and antagonist muscle groups. The body linkage then moves in the shortest way possible to the new location of agonist / antagonist equilibrium with muscles responding like springs to any unexpected variables (Polit & Bizzi, 1978; Pew & Rosenbaum, 1988; Bizzi & Mussa-Ivaldi, 1989). Compatible models have developed for the motor control of speech articulations where phonemes are produced by recalling tongue-mouth positions rather than movements (MacNeilage, 1970). These effects indicate that location information is used at an elemental stage by the motor system.
According to the model of “trajectory formation” sequences of locations are linked into polygonal representations of movement paths. Measurements of spatial path curvature and velocity during relatively unrestrained multi-joint arm movements indicate that curved movements occur as a series of approximately straight “path segments” separated by “curvature peaks” (a slight bump in the curving pathway). The velocity of the hand exhibits a corresponding pattern, being faster during the path segments and slower during each curvature peak. This occurs in planar movements (Abend, Bizzi & Morasso, 1982), three-dimensional movements (Morasso, 1983b) and is duplicated in simultaneous trajectories of different body parts (shoulder, hand) involved in the same movement (Morasso, 1986). A model for the production of spatial paths was developed in which the overall curvature is produced from a series of relatively straight path segments (Morasso, Mussa-Ivaldi & Ruggiero, 1983; Morasso, 1986). Each path segment is considered to be a “stroke” and a series of strokes to be “the sides of the polygon”. Spatial trajectories are cognitively planned as a polygonal shape with the vertices of the polygon serving as “guiding points” (elemental loci) and appearing as curvature peaks within the bodily recall of the trajectory. When strokes are performed in a discontinuous manner then angular transitions occur at the curvature peaks. When the strokes are overlapped or superimposed, beginning the next stroke before the last one is finished, then smoothly curving peaks occur.
This method for generating curved lines from a series of straight vectors is similar to “spline functions” used in computer graphics. Compatible models have developed where the size of handwriting is changed by increasing or decreasing the duration of all the strokes by the same proportion, without any change to the overall shape of the polygonal form (Viviani & Terzuolo, 1980; Wing, 1980).
Laban also observed this same characteristic of peaks and phases in motor behaviour and developed a choreutic conception virtually identical to the trajectory formation model. Choreutic paths are described according to observable “peaks” within a trajectory and “phases of its pathway”. When the peaks are grouped together the trajectory as a whole is conceived as being polygonal (“hexagonal”, “heptagonal”, etc., with one peak at each polygonal corner) and to create “spatial rhythm” or “polygonal rhythm”. Curved or angular trajectories are produced from the same polygonal representation, depending on whether successive strokes are smoothly blended together or if the peaks are abruptly accented (Laban, 1966, pp. 22–28, 46–47).
Cognitive Maps
When spatial information is well learned, individual locations and trajectories typically link together in memory to form map-like images which represent an entire spatial environment. Cognitive maps are indicated in behaviors such as being able to judge the way to a known destination across a path which itself has never before been experienced (‘short–cut’) just as if reading the information from a mental map (Tolman, 1948; Neisser, 1976; Levine, Jankovic & Palij, 1982; Moar & Carleton, 1982).
The cognitive mapping model typically refers to large–scale environments but it can be applied to any size of space ranging from buildings within a city, objects in a room, drawings on a piece of paper, and directions of body parts (Souder, 1972, p. 14; Siegel & White, 1975, p. 13; Neisser; 1976, pp. 113, 123; Stelmach & Larish, 1980, p. 168; Hintzman, O’Dell & Arndt, 1981, p. 155). Mapping analogies are also used in motor control research to describe perception and memory of body movement and positions where spatial landmarks are identified according to anatomical structures and proprioceptive sensations (Paillard & Brouchon, 1974, p. 283; Saltzman, 1979, p. 113; Heister, Schroeder-Heister & Ehrenstein, 1990).
Body space is fundamental to all sizes of cognitive maps. Tasks in one size of space (placing objects on a piece of paper, drawing a map) are typically taken as models for behaviour in another size of space (memory of buildings and roads in a large city). Thus, it is often eye and arm movements (pointing or drawing) which are used for learning and recalling small–scale spaces (Stevens & Coupe, 1978; Hintzman et al., 1981; Thorndyke, 1981; Moar & Carleton, 1982; McNamara, Hardy, & Hirtle, 1989) and also large–scale spaces (Levine, et al., 1982; Presson & Hazelrigg, 1984). Similarly, eye movements will trace paths and establish landmarks (by repeated visits) in a small space (eg. a painting) in the same manner as locomotion does in larger spaces (Hochberg, 1975). The use of body movements across various spatial mapping tasks, and similar mapping analogies for body space and large scale environmental space, suggest a continuity of representation across sizes of space and that the mapping analogy is appropriately applied throughout.
Choreutics also uses a mapping analogy when considering mental images of body movements and positions. This realm is referred to as the “kinesphere”, defined as “the sphere around the body whose periphery can be reached by easily extended limbs” (Laban, 1966, p. 10) and is essentially identical to the “workspace”, “reach space”, and “kinetosphere” etc. as used in ergonomics (Dempster, Gabel & Felts, 1959; Damon, Stoudt & McFarland, 1966; Pheasant, 1986).
One of the distinctive features of choreutics is the use of polyhedra overlaid onto the kinesphere to provide a conceptual network of spatial coordinates or “orientation points” used to represent movements in “point-to-point” sequences (Laban, 1926, p. 11, 21–22) or, specifically as “routes” within polyhedral “maps” (Bartenieff & Lewis, 1980, p. 29; Moore, 1982, pp. 68–69; Salter, 1983, p. 166). These polyhedra nets are described as “scaffolding” (Laban, 1966, pp. 68, 101-107, 124), or a “grid” (Preston-Dunlop, 1984) and are comparable to the “net of the motor field” (Bernstein, 1984, p. 109). The five regular polyhedra are used as nets most often (the most symmetrical divisions of Euclidean space) though other irregular polyhedra are also used (Laban, 1984).
Simple kinespheric networks have been typically used in many fields of body study. The fundamental net, derived from the three axes of a Cartesian coordinate system and the corresponding three Cartesian planes, is commonly used in kinesiology to specify positions and movements of body-parts. However, joining these into polyhedral nets which are used as maps of movement routes appears to be unique to choreutics. Cubic nets are sometimes used, for example as a “space module” for the spatial representation of ballet (Kirstein & Stuart, 1952, pp. 2, 20, 30) but this never approaches the sophistication of polyhedral networks. Kinespheric nets are compatible with neural networks designed for spatial-motor cognition in artificial intelligence systems with spatial targets represented as networks of “attractor fields” (Morasso & Sanguineti, 1995; Sanguineti & Morasso, 1997) and transformations of spatial sequences (eg. size scaling) facilitated by deriving “transient information” (motions) from a series of loci (Ans, Coiton, Gilhodes, & Velay, 1994).
 |
|
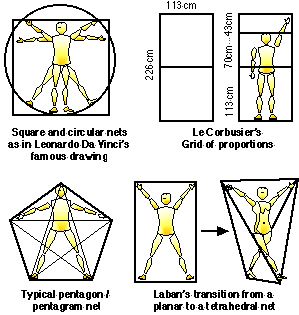
Figure 1. Examples of planar kinespheric networks. |
Figure 1 gives examples of planar networks which have a long tradition of use for defining body proportions by artists (Heydenreich, 1928, p. 110; Strauss, 1974, pp. 2426-2477; Ghyka, 1977, pp. 97–109; Doczi, 1981, pp. 93–143). The architect and painter ‘Le Corbusier’ used a frontal planar net as a “grid of proportions”, “designed to fit the man placed within it” and provide a body–scaled measurement system (Le Corbusier, 1980, pp. 37–58). Two of the most typical kinespheric nets in the frontal plane are pentagon-shaped (5 nodes: head, two hands, two feet) and quadrangular-shaped (4 nodes: two hands, two feet). When the arms and legs are no longer in the same plane then the planar spatial form molds into a plastic volume, the most simple is conceived in choreutics as a tetrahedral net with four limbs or four proximal joints each at one of the four tetrahedral vertices (Laban, 1966, pp. 18–21; Bartenieff & Lewis, 1980, pp. 97–99, 113).
 |
|
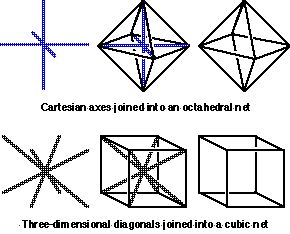
Figure 2. Octahedral (cardinal directions) and cubic kinespheric nets. |
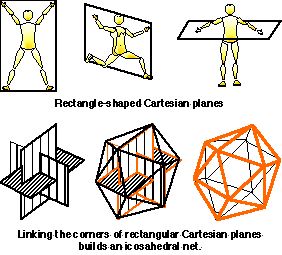
In figure 2 the octahedral net (6 vertices) is formed by linking the six directions of the Cartesian cross. The eight directions midway between the axes of the Cartesian cross are then linked into a cubic net (8 vertices) (Laban, 1966, pp. 11-16, 103-104). A choreutic tenet posits that planar body movements do not occur equally in all directions so that the Cartesian planar nets are not square but are each lengthened along one of the dimensions (Laban, 1926, pp. 22-23; 1966, pp. 101-102; Ullmann; 1966, pp. 139–142; 1971, pp. 18-21; Bartenieff & Lewis 1980, p. 32; Preston-Dunlop, 1984, pp. 21-22). This is in general accord with ergonomic measurements of the shape of the workspace (Squires, 1956; Dempster et al., 1959; Goel, 1968). Figure 3 displays how the corners of these three rectangular–shaped Cartesian planes are joined to create an icosahedral net (12 vertices).
 |
|
Figure 3. Icosahedral kinespheric net. |
Spatial Transformation
Crucial for effective everyday spatial behaviour is the ability to transform spatial information according to various operations (eg. mental rotation, reflection, imagined self-translation). Reaching for an object without looking at it requires that the spatial image of the environment be continually rotated and translated relative to the ongoing movements of one’s body. To give directions from a real or imagined map it must be physically or mentally rotated to fit the environment (Hardwick et al., 1976; Hintzman et al., 1981). An object’s visual image will have various sizes and shapes when reaching the eye depending on its orientation and distance relative to the observer. This visual image must be appropriately rotated and scaled in size for the object to be recognised (Rock, 1973). In child development these “operative” cognitive abilities (manipulation of spatial images) gradually emerge from more fundamental “figurative” abilities of static imagery (Piaget & Inhelder, 1967; 1971).
Transformational operations are also models for organising information into higher–order groupings which increase memory capacity by unitizing large numbers of individual items into small numbers of “clusters” or “chunks” (Miller, 1956; Tulving, 1962; Reitman & Rueter, 1980; Richman, Gobet, Staszewski, & Simon, 1996). It is convenient and economic to organise items into clusters based on their repetitions, mirroring, and translated relationships (Restle & Burnside, 1972; Inhoff, Rosenbaum, Gordon & Campbell, 1984), whereby all the members of a cluster could be generated by applying a single transformational ‘rule’ to an initial item (Greeno & Simon, 1974; Collard & Povel, 1982; Gordon & Meyer, 1987).
In translation operations a spatial item (eg. the orientation of a line) is recalled in a new location. In spatial-motor recall translations often occur together with size scaling and at least a small transfer in the bodily–muscular use which is recalling the item (Bernstein, 1984, p. 109). A common example is handwriting styles which are retained regardless of various body transfers and sizing (Merton, 1972, p. 32; Wing, 1980; Schmidt, 1982, p. 305; Bernstein, 1984, pp. 106-114; Smyth & Wing, 1984, p. 12). Spatial information is also automatically translated between eye movements and arm-hand movements (Angel, Hollander & Wesley, 1973; Levine et al., 1982, p. 166), between the shoulder and the hand in trajectories where one spatial form “mimics” the other (Morasso, 1986, pp. 23-24, 34-35) or between walking a path and drawing it (Levine et al., 1982). These operations can commonly be observed in dancers who rehearse spatial sequences with the arms and then translate and enlarge these into leg movements.
Reflection operations occur when a spatial item (eg. a body pose) is recalled with all directions reversed across a reflection plane. Bilateral reflection is more typical than vertical and sagittal reflections (eg. right/left reflection errors when learning to write; Bernstein, 1984, p. 108) since the bilateral symmetry present within the human body makes right/left confusions likely (Corballis & Beale, 1970; Rock, 1973, pp. 19–20). Right/left reflections are often accompanied with a right/left bodily transfer without any decrement to spatial recall (Wallace, 1977; Stelmach & Larish, 1980; Larish & Stelmach, 1982) and this dual operation is commonly referred to in dance as ‘the other side’.
The ease of some translation, sizing, and reflection operations indicates that different body parts are functionally linked within the nervous system. A single spatial form can be precisely reproduced by another body part within 1° of accuracy (Gibson & Backlund, 1963, p. 148; Willott, 1973, p. 578) but it is difficult to recall two different spatial forms simultaneously (eg. pat your head and rub your stomach) (Smyth, Morris, Levy, & Ellis, 1987, pp. 97-100). In studies of “bilateral transfer”, “indirect learning”, or “transfer of training” experience of one body half (right or left) is automatically transferred to the other half (Hellebrandt & Waterland, 1962; Laszlo & Baguley, 1971; Roy & Williams, 1979; Smyth & Pendleton, 1989). The ease of translation and sizing operations can also be attributed to these occurring a later stage in the movement recall process whereas changing directions (in reflection or rotation) can be more difficult since the entire recall process must be reinitiated from the beginning (Larish & Frekany, 1985).
In rotation operations a spatial item (eg. the direction towards an object) is recalled in a new orientation. Mental rotation operations are indicated by the predictable increases in time required to visually compare differently orientated spatial figures (Shepard & Metzler, 1971; Cooper & Shepard, 1984) or for congenitally blind subjects who tactually compare the shapes of figures (Marmour & Zaback, 1976; Carpenter & Eisenberg, 1978). Rotation is in addition to the time required for mental size scaling operations when the images are also different sizes (Sekuler & Nash, 1972; Bundesen, Larsen & Farrell, 1981). Spatial items (eg. a picture, an action) are often recalled best in a particular orientation (Rock, 1973, pp. 34–49; Levine et al., 1982) however when the information is learned from a variety of perspectives then this orientation specificity diminishes (Evans & Pezdek, 1980; Hintzman et al., 1981; Presson & Hazelrigg, 1984; Presson, DeLange & Hazelrigg, 1987).
Abilities in all types of spatial-motor transformations are cultivated in dance practice and choreography (Blom & Chaplin, 1982, pp. 102–104; Wechsler, 1990; Forsythe, 1999) and are implicit in ballet pedagogy and terminology (Grant, 1982). Specialised notation symbols have also been created for the operations most commonly used (Hutchinson, 1970, pp. 346–359).
 |
|
Figure 4. Transforming a 3-ring in an octahedral kinespheric net. |
Spatial transformations are fundamental to choreutics. Figure 4 illustrates the practice of learning a spatial pattern (eg. a triangle) and recalling it in new transformations (Laban, 1966, pp. 68-82; Ullmann, 1966, pp. 152-170; Preston–Dunlop, 1984; Longstaff, 1989). Choreutic ‘scales’ (analogous to musical scales) are derived by systematically repeating a simple form through many possible orientations which, when linked into a continuous sequence, exhibit three-dimensional symmetries. These scales give symmetrical solutions to variations of Hamilton’s and Euler’s geometric puzzles. In Hamilton’s “Icosian Game” (circa 1850) the player moves through a series of polyhedral vertices, visiting each only once, and attempting to end at the same place where one began (Hankins, 1980, pp. 339–343; O’Donnell, 1983). Euler’s Koenigsberg bridge problem (circa 1750) asked whether it is possible to take a walk in the town of Koenigsberg crossing every bridge once and returning home at the end (Ball, 1905, p. 167). Similarly, the “traveling salesman problem” searches for the shortest route which visits each city once within a given set.
Choreutic scales are not intended solely as generating systems for symmetrical polyhedral patterns but are hypothesised to be prototypes for spatial sequences occurring during equilibrium reflexes. Movement away from the centre of balance induces a reflex counter–movement in order to automatically maintain balance (Crowe, Porrill, & Prescott, 1998). This can move the body into a new direction which itself requires another reflex counter-movement to maintain balance. In this “dynamic equilibrium” each movement serves as a balancing reaction to the last (Rasch & Burke, 1978, p. 102). The paths and direction changes in choreutic scales are considered to be prototypical examples of this act-react reflex pattern (Laban, 1926, pp. 18, 29; 1966, pp. 89-90). Accordingly, the mental conception and physical execution of the scales is recommended as a “prescriptive” system of training (Salter, 1977, p. 138) since they guide experience over an entire range of cognitive and bodily possibilities.
Deformations of Topological Forms
In an analysis of spatial forms produced by body movements (eg. handwriting) the famous Soviet cyberneticist N. Bernstein (1984, pp. 102-117) considered the importance of the distinction between topological and metric properties. Metric properties consist of specific sizes, proportions, and degrees of angle or curvature, whereas topological properties consist of the overall shape of a figure regardless of its specific size or measurements, whether a figure is closed or open, if lines intersect or not, which features are next to each other, or if one figure completely surrounds or encloses another. Bernstein also designates, “topological properties of the first order” which include the number of features (eg. angles, crossing lines) which are present in a figure.
A basic issue in spatial cognition considers how spatial forms (eg. letters) can be bodily recalled and visually recognised in spite of considerable variation (individual handwriting ‘style’). Similarly, in many instances of spatial transformations (eg. sizing, transferring body use) the transformed spatial items can be recalled and recognised as simply and easily as the original. According to the “principle of motor equivalence” (Morasso, 1983a, pp. 208–209; Saltzman, 1979, pp. 94, 103) or Bernstein’s (Ibid) “principle of equal simplicity” this equivalent simplicity or ease by which a range of variations can be recalled indicates that these are all produced from the same mental representation. Bernstein argues that this “abstract motor image of space” is composed of topological properties rather than being based on metric quantities or the bodily use during learning and recall.
Furthermore, Bernstein observed that a spatial form will never have identical measurements each time it is recalled, but will always be recalled at least somewhat larger or smaller, more angular or more curved, depending on the conditions operating at each moment. Similarly, even intentionally straight point-to-point arm motions spontaneously deviate into three-dimensional curvatures (Pollick & Ishimura, 1996). Bernstein (Ibid) characterised these continual metric deformations of topological forms as the “co-ordinational net of the motor field . . . as oscillating like a cobweb in the wind”. These oscillations are the metric stretching and bending of a spatial form on each successive execution while the essential topological structure remains unchanged.
 |
|
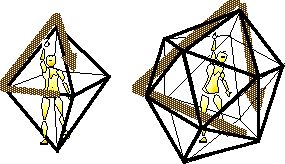
Figure 5. Deflecting / oscillating a 3-ring between octahedral and icosahedral kinespheric networks. |
The choreutic principle of “deflection” is quite similar to Bernstein’s “oscillation”. A choreutic form (eg. the hexagonal “defense sequence”) might be recalled with various deformations of its prototypical shape (Laban, 1966, pp. 37–42). Many of the choreutic scales and rings can be identified as deflected variations of the same topological form (Ullmann, 1971, pp. 18-26; Longstaff, 1996, pp. 207-220, 251-261). Figure 5 illustrates how deflections (oscillations) are conceived in choreutics by mapping a single topological form according to various kinespheric nets.
The choreutic conception of the bodily production of spatial forms is given psychological validation from the finding that its major conceptual structures are closely similar to models of spatial learning and memory developed in motor control and cognitive science. These commonalities indicate that further critical reexaminations of “choreutic laws” might be useful for suggesting conceptual models of spatial cognitive processes and in identifying attributes for movement analysis. These can be evaluated in practical studies of motor learning and in deciphering a stylistic free and psychologically valid taxonomy of whole-body movements which is needed in psychological studies (Whiting, 1986, pp. 116, 124) and in artificial intelligence systems (Camurri, 1997).
Abend, W. E., Bizzi, E, & Morasso, P. (1982) Human arm trajectory formation. Brain, 105, 331–348.
Angel, R. W., Hollander, M., & Wesley, M. (1973) Hand-eye coordination: The role of “motor memory”. Perception & Psychophysics, 14 (3), 506–510.
Ans, B., Coiton, Y., Gilhodes, J., & Velay, J. (1994) A neural network model for temporal sequence learning and motor programming. Neural Networks, 7 (9), 1461-1476.
Ball, W. W. (1905) Mathematical recreations and essays. 4th edition. New York: MacMillan.
Bartenieff, I., & Lewis, D. (1980) Body movement; coping with the environment. New York: Gordon and Breach.
Bernstein, N. (1984) The problem of the interrelation of co–ordination and localization. In H. T. A. Whiting (Ed.), Human motor actions; Bernstein reassessed. New York: North Holland (pp. 77-119). (Originally published 1935; Also published in Bernstein, N. [1967] The Co-ordination and regulation of movements. Oxford: Pergamon Press [pp. 15-59].)
Bizzi, E., & Mussa-Ivaldi, F. A. (1989) Geometrical and mechanical issues in movement planning and control. In M. I. Posner (Ed.), Foundations of cognitive science. Cambridge Massachusetts: M. I. T. Press (pp. 769-792).
Blom, L. A., & Chaplin, L. T. (1982) The intimate act of choreography. Pittsburgh, PA: University of Pittsburgh Press.
Bodmer, S. (1974) Harmonics in space. Maincurrents in Modern Thought, 31 (1), 27-31.
Bodmer, S. (1979) Studies based on crystalloid dance forms. Notations by J. Siddall. Laban Centre: London.
Bower, G. H. (1970) Analysis of a mnemonic device. American Scientist, 58, 496–510.
Broadbent, D. E., and Broadbent, M. H. P. (1981) Recency effects in visual memory. Quarterly Journal of Experimental Psychology, 33A, 1–15.
Brody, L. (1995) The art of movement: try kinespherics [Kristine Lindahl]. Shape, April, 100-105.
Bundesen, C., Larsen, A., & Farrell, J. E. (1981) Mental transformations of size and orientation. In J. Long and A. Baddeley (Eds.), Attention and performance IX. Hillsdale, NJ: Lawrence Erlbaum (pp. 279-294).
Camurri, A. (1997) Network models in motor control and music. In P. Morasso & V. Sanguineti (Eds.), Self-organization, Computational Maps, and Motor Control. Amsterdam: Elsevier Science B. V. (pp. 311-355).
Camurri, A., Morasso, P., Tagliasco, V., & Zaccaria, R. (1986) Dance and movement notation. In P. Morasso and V. Tagliasco (Eds.), Human movement understanding. New York: North Holland (pp. 85-124).
Carpenter, P. A., & Eisenberg, P. (1978) Mental rotation and the frame of reference in blind and sighted individuals. Perception & Psychophysics, 23 (2), 117-124.
Collard, R., & Povel, D. J. (1982) Theory of serial pattern production: tree traversals. Psychological Review, 89 (6), 693-707.
Cooper, L. A., & Shepard, R. N. (1984) Turning something over in the mind. Scientific American, 251 (6), 114-120.
Corballis, M. C., & Beale, I. L. (1970) Bilateral symmetry and behavior. Psychological Review, 77 (5), 451-464.
Crowder, R. G. (1978) Mechanisms of auditory backward masking in the stimulus suffix effect. Psychological Review, 85 (6), 502-524.
Crowe, A., Porrill, J., & Prescott, T. (1998) Kinematic coordination of reach and balance. Journal of Motor Behavior, 30 (3), 217-233.
Damon, A., Stoudt, H. W., & McFarland, R. A. (1966) The human body in equipment design. Cambridge, MA: Harvard University Press.
Davis, M. (1987) Steps to achieving observer agreement: the LIMS reliability project. Movement Studies, 2, 7-19. (New York: Laban Institute of Movement Studies)
Dell, C. (1972) Space harmony basic terms. Revised by A. Crow (1969). Revised by I. Bartenieff (1977). New York: Dance Notation Bureau.
Dempster, W. T., Gabel, W. C., & Felts, W. J. L. (1959) The anthropometry of the manual work space for the seated subject. American Journal of Physical Anthropology, 17, 289-317.
Doczi, G. (1981) The power of limits, proportional harmonies in nature, art, and architecture. Boulder, CO: Shambhala.
Evans, G. W., & Pezdek, K. (1980) Cognitive mapping: knowledge of real-world distance and location information. Journal of Experimental Psychology: Human Learning and Memory, 6 (1), 13–24.
Forsythe, W. (1999) William Forsythe Improvisation Technologies (CD ROM and booklet). Karlsruhe: Zentrum für Kunst und Medientechnologie.
Ghyka, M. (1977) The geometry of art and life. New York: Dover. (First published 1946.)
Gibson, J. J., & Backlund, F. A. (1963) An after-effect in haptic space perception. The Quarterly Journal of Experimental Psychology, 15, 145-154.
Goel, S. C. (1968) An anthropometric study of the shape of the normal work area in the horizontal plane. M. S. Thesis, dept. of Industrial Engineering: Kansas State University.
Golani, I. (1986) What are the building blocks of the frog’s wiping reflex? Behavioral and Brain Sciences, 9, 607-608.
Gordon, P. C., & Meyer, D. E. (1987) Control of serial order in rapidly spoken syllable sequences. Journal of Memory and Language, 26, 300–321.
Grant, G. (1982) Technical manual and dictionary of classical ballet. 3rd revised edition. New York: Dover.
Green, M. (1986) Mountain of truth; the counterculture begins, Ascona, 1900-1920. Hanover, NH: University Press of New England.
Greeno, J. G., & Simon, H. (1974) Processes for sequence production. Psychological Review, 81 (3), 187-197.
Hankins, T. L. (1980) Sir William Rowan Hamilton. Baltimore, MD: Johns Hopkins University Press.
Hardwick, D. A., McIntyre, C. W., & Pick, H. L. Jr. (1976) The content and manipulation of cognitive maps in children and adults. Monographs of the Society for Research in Child Development, 41 (3), Serial No. 166), 1-55.
Heister, G., Schroeder-Heister, P., & Ehrenstein, W. H. (1990) Spatial coding and spatio-anatomical mapping: Evidence for a hierarchical model of spatial stimulus-response compatibility. In R. W. Proctor and T. G. Reeve (Eds.), Stimulus-response compatibility. Amsterdam: North Holland (pp. 117-143).
Hellebrandt, F. A., Schade, M., & Carns, M. L. (1962) Methods of evoking the tonic neck reflexes in normal human subjects. American Journal of Physical Medicine, 41, 90–139.
Hellebrandt, F. A., & Waterland, J. C. (1962) Indirect learning. The influence of unimanual exercise on related muscle groups of the same and the opposite side. American Journal of Physical Medicine, 41, 45-55.
Heydenreich, L. H. (1928) Leonardo Da Vinci; Vol. II: plates. New York: MacMillan. (First English edition, 1954.)
Hill, H. (1996) An attempt to describe and understand moments of experiential meaning within the dance therapy process. Ann Arbor: UMI. (M. E. Thesis, La Trobe University, Australia, 1995.)
Hinton, G. E., & Parsons, L. M. (1981) Frames of reference and mental imagery. In J. Long and A. Baddeley (Eds.), Attention and performance IX. Hillsdale, NJ: Lawrence Erlbaum (pp. 261-277).
Hintzman, D. L., O’Dell, C. S., & Arndt, D. R. (1981) Orientation in cognitive maps. Cognitive Psychology, 13, 149-206.
Hochberg, J. (1975) Motion pictures, eye movements, and mental maps: Perception as purposive behavior. Address presented at the American Psychological Association. Chicago. (Reviewed by Neisser, 1976, pp. 123-124.)
Humphreys, G. W. (1983) Reference frames and shape perception. Cognitive Psychology, 15, 151-196.
Hutchinson, A. (1970) Labanotation or kinetography Laban: the system of analyzing and recording movement. 3rd revised edition (1977). New York: Theatre Arts Books.
Hutchinson-Guest, A. (1989). Choreo-Graphics; A Comparison of Dance Notation Systems from the Fifteenth Centrury to the Present. New York: Gordon and Breach.
Inhoff, A. W., Rosenbaum, D. A., Gordon, A. M., & Campbell, J. A. (1984) Stimulus-response compatibility and motor programming of manual response sequences. Journal of Experimental Psychology: Human Perception and Performance, 10 (5), 724-733.
Kelso, J. A. S. (1977) Motor control mechanisms underlying human movement reproduction. Journal of Experimental Psychology: Human Perception and Performance, 3 (4), 529-543.
Kirstein, L., & Stuart, M. (1952) The classic ballet. New York: Alfred A. Knopf. (Twenty-second printing 1986.)
Knust, A. (1979) Dictionary of kinetography Laban (Labanotation). Estover, Plymouth: MacDonald and Evans.
Laban, R. (1926) Choreographie. Jena: Eugen Diederichs. (Unpublished English edition translated by J. Longstaff and E. Zierach. [1993]. London: Laban Centre; Laban Collection.)
Laban, R. (1966) Choreutics. Annotated and edited by L. Ullmann. London: MacDonald and Evans. (Published in U.S.A. as The language of movement; a guide book to choreutics. Boston, MA: Plays.)
Laban, R. (1975) Laban’s principles of dance and movement notation. 2nd edition edited and annotated by R. Lange. London: MacDonald and Evans.
Laban, R. (1980) The mastery of movement. 4th edition revised and enlarged by L. Ullmann. London: MacDonald and Evans. (First published as The mastery of movement on the stage, 1950.)
Laban, R. (1984) A vision of dynamic space. Compiled by L. Ullmann. London: The Falmer Press.
Laban, R., & Lawrence, F. C. (1947) Effort. London: MacDonald and Evans. (4th reprint 1967.)
Lamb, W. (1965) Posture and gesture; an introduction to the study of physical behaviour. London: Gerald Duckworth.
Langer, S. K. (1953) Feeling and form. London: Routledge & Kegan Paul.
Larish, D. D. & Frekany, G. A. (1985) Planning and preparing expected and unexpected movements: reexamining the relationships of arm, direction, and extent of movement. Journal of Motor Behavior, 17 (2), 168-189.
Larish, D. D., & Stelmach, G. E. (1982) Spatial orientation of a limb using egocentric reference points. Perception & Psychophysics, 32 (1), 19-26.
Laszlo, J. I, & Baguley, R. A. (1971) Motor memory and bilateral transfer. Journal of Motor Behavior, 3 (3), 235-240.
Le Corbusier [Jeanneret-Gris, C. E.] (1980) Modulor I and II. Cambridge, MA: Harvard University Press.
Lehtiö, P. K., Poikonen, L., & Tuunainen, K. (1980) Retrieval of information from a mental map. In R. S. Nickerson (Ed.), Attention and performance VIII. Hillsdale, NJ: Lawrence Erlbaum (pp. 381–392).
Lepczyk, B. (1992). Towards a quantitative analysis of classic ballet: the upper body technique viewed through choreutics. In L. Y. Overby and J. H. Humphrey (Eds.), Dance: current selected research volume 3. New York: AMS press (pp. 103-188).
Levine, M., Jankovic, I. N., & Palij, M. (1982) Principles of spatial problem solving. Journal of Experimental Psychology: General, 111 (2), 157-175.
Levinson, S. C. (1996) Frames of reference and Molyneux’s question: cross linguistic evidence. In P. Bloom, M. A. Peterson, L. Nadel, & M. F. Garrett (Eds.), Language and space. Cambridge MA: MIT press (pp. 112-169).
Loman, H. (1987) Classwork for professional dancers. South Croydon, Surrey: Croydon Dance Theatre.
Lomax, A., Bartenieff, I., & Paulay, F. (1968) The choreometric coding book. In A. Lomax (Ed.), Folk song style and culture. New Brunswick, NJ: Transaction Books (pp. 262-273).
Longstaff, J. S. (1989) Moving in crystals: a continued integration of polyhedal geometry with Rudolf Laban’s choreutics. Eugene, Oregon: Microform Publications, College of Human Development and Performance. (M. S. Thesis, University of Oregon, 1988.)
Longstaff, J. S. (1996) Cognitive structures of kinesthetic space: reevaluating Rudolf Laban’s choreutics. Ph.D. Thesis. City University London; Laban Centre London.
Longstaff, J. S. (1998) Subjective organisation in the recall of abstract body movements. Perceptual and Motor Skills, 86, 931-940.
MacNeilage, P. F. (1970) Motor control of serial ordering of speech. Psychological Review, 77 (3), 182-196.
Maletic, V. (1987) Body - space - expression; the development of Rudolf Laban’s movement and dance concepts. Berlin: Mouton de Gruyter.
Mandler, J. M., Seegmiller, D., and Day, J. (1977) On the coding of spatial information. Memory & Cognition, 5 (1), 10-16.
Marmour, G. S., & Zaback, L. A. (1976) Mental rotation by the blind: Does mental rotation depend on visual imagery? Journal of Experimental Psychology: Human Perception and Performance, 2 (4), 515–521.
Marr, D. (1980) Visual information processing: the structure and creation of visual representations. Philosophical Transactions of the Royal Society of London, Series B, 290, 199-218.
McFarland, J. H., Werner, H., & Wapner, S. (1962) The effect of postural factors on the distribution of tactual sensitivity and the organization of tactual-kinaesthetic space. Journal of Experimental Psychology, 63 (2), 148-154.
McNamara, T. P., Hardy, J. K., & Hirtle, S. C. (1989) Subjective hierarchies in spatial memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 15 (2), 211-227.
Merton, P. A. (1972) How we control the contraction of our muscles. Scientific American, May, 30-37.
Miller, G. A. (1956) The magical number seven, plus or minus two: Some limits on our capacity for processing information. The Psychological Review, 63 (2), 81-97.
Moar, I., & Carleton, L. R. (1982) Memory for routes. Quarterly Journal of Experimental Psychology, 34A, 381-394.
Moore, C. L. (1982) Executives in action: a guide to balanced decision–making in management. Estover, Plymouth: MacDonald & Evans.
Morasso, P. (1983a) Coordination aspects of arm trajectory formation. Human Movement Science, 2, 197-210.
Morasso, P. (1983b) Three dimensional arm trajectories. Biological Cybernetics, 48, 187-194.
Morasso, P. (1986) Trajectory formation. In P. Morasso and V. Tagliasco (Eds.), Human movement understanding. Amsterdam: North Holland (pp. 9–55).
Morasso, P., Mussa-Ivaldi, F. A., & Ruggiero, C. (1983) How a discontinuous mechanism can produce continuous patterns in trajectory formation and handwriting. Acta Psychologica, 54, 83–98.
Morasso, P., & Sanguineti, V. (1995) Self-organizing body schema for motor planning. Journal of Motor Behavior, 27 (1), 52-66.
Neisser, U. (1976) Cognition and reality. San Francisco: W. H. Freeman.
North, M. (1972) Personality assessment through movement. London: MacDonald and Ev
 ans.
ans.
O’Donnell, S. (1983) William Rowan Hamilton: portrait of a prodigy. Dublin: Boole Press.
Paillard, J. (1987) Cognitive versus sensorimotor encoding of spatial information. In P. Ellen, and C. Thinus–Blanc (Eds.), Cognitive processes and spatial orientation in animal and man. vol. ii neurophysiology and developmental aspects. Dordrecht, The Netherlands: Martinus Nijhoff (pp. 43-77).
Paillard, J., & Brouchon, M. (1974) A proprioceptive contribution to the spatial encoding of position cues for ballistic movements. Brain Research, 71, 273–284.
Paivio, A. (1979) Imagery and verbal processes. Hillsdale, New Jersey: Lawrence Erlbaum.
Pew, R. W., & Rosenbaum, D. A. (1988) Human movement control: Computation, representation, and implementation. In R. C. Atkinson, R. J. Herrnstein, G. Lindzey, and R. D. Luce (Eds.), Stevens’ handbook of experimental psychology; vol. 2. learning and cognition (2nd ed.). New York: John Wiley (pp. 473-509).
Pezdek, K., Roman, Z., and Sobolik, K. G. (1986) Spatial memory for objects and words. Journal of Experimental Psychology: Learning, Memory, and Cognition, 12 (4), 530-537.
Pheasant, S. (1986) Bodyspace; anthropometry, ergonomics and design. London: Taylor and Francis.
Piaget, J., & Inhelder, B. (1967) The child’s conception of space. New York: W. W. Norton.
Piaget, J., & Inhelder, B. (1971) Mental imagery in the child. New York: Basic Books.
Polit, A., & Bizzi, E. (1978) Processes controlling arm movements in monkeys. Science, 201 (Sept.), 1235-1237.
Pollick, F. E., & Ishimura, G. (1996) The three-dimensional curvature of straight-ahead movements. Journal of Motor Behavior, 28 (3), 271–279.
Presson, C. C., DeLange, N., & Hazelrigg, M. D. (1987) Orientation-specificity in kinesthetic spatial learning: The role of multiple orientations. Memory & Cognition, 15 (3), 225–229.
Presson, C. C., & Hazelrigg, M. D. (1984) Building spatial representations through primary and secondary learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 10 (4), 716–722.
Preston-Dunlop, V. (1969) Practical kinetography Laban. London: MacDonald and Evans.
Preston-Dunlop, V. (1981) The nature of the embodiment of choreutic units in contemporary choreography. Ann Arbor, MI: University Microfilms International. (Ph.D. Thesis. London: Laban Centre.)
Preston-Dunlop, V. (1984) Point of departure: the dancer’s space. London: 64 Lock Chase, SE3, Author.
Preston-Dunlop, V. (1998) Rudolf Laban: an extraordinary life. London: Dance Books.
Rasch, P. J., & Burke, R. K. (1978) Kinesiology and applied anatomy (6th ed.). Philadelphia: Lea & Febiger.
Reitman, J. S., & Reuter, H. H. (1980) Organization revealed by recall orders and confirmed by pauses. Cognitive Psychology, 12, 554–581.
Restle, F., & Burnside, B. L. (1972) Tracking of serial patterns. Journal of Experimental Psychology, 95 (2), 299-307.
Richman, H. B., Gobet, F., Staszewski, J. J., & Simon, H. A. (1996) Perceptual and memory processes in the acquisition of expert performance: the EPAM model. In K. A. Ericsson (Ed.), The road to excellence. Mahwah NJ: Lawrence Erlbaum (pp. 167-187).
Rieser, J. J., & Pick, H. L. Jr. (1976) Reference systems and the perception of tactual and haptic orientation. Perception & Psychophysics, 19 (2), 117-121.
Rock, I. (1973) Orientation and form. New York: Academic Press.
Rothkopf, E. Z., Fisher, D. G., and Billington, M. J. (1982) Effects of spatial context during acquisition of the recall of attributive information. Journal of Experimental Psychology: Learning, Memory, and Cognition, 8 (2), 126-138.
Roy, E. A. (1977) Spatial cues in memory for movement. Journal of Motor Behavior, 9 (2), 151-156.
Roy, E. A., & Williams, I. D. (1979) Memory for location and extent: The influence of reduction of joint feedback information. In G. C. Roberts and K. M. Newell (Eds.), Psychology of motor behavior and sport - 1978. Champaign, IL: Human Kinetics (pp. 229–240).
Russell, D. G. (1976) Spatial location cues and movement production. In G. E. Stelmach (Ed.), Motor control issues and trends. New York: Academic Press (pp. 67–83).
Salter, A. (1977) The curving air. London: Human Factors Associates.
Salter, A. (1983) Dance and the quasi-personal in art. Ph.D. Thesis. London: Laban Centre.
Saltzman, E. (1979) Levels of sensorimotor representation. Journal of Mathematical Psychology, 20, 91-163.
Sanguineti, V., & Morasso, P. (1997) Computational maps and target fields for reaching movements. In P. Morasso & V. Sanguineti (Eds.), Self-organization, Computational Maps, and Motor Control. Amsterdam: Elsevier Science B. V. (pp. 507-546).
Schmidt, R. A. (1982) Motor control and learning a behavioral emphasis. Champaign Illinois: Human Kinetics.
Sekuler, R., & Nash D. (1972) Speed of size scaling in human vision. Psychonomic Science, 27 (2), 93-94.
Shepard, R. N., & Metzler J. (1971) Mental rotation of three-dimensional objects. Science, 171 (Feb.), 701-703.
Siegel, A. W., & White, S. H. (1975) The development of spatial representations of large-scale environments. In H. W. Reese (Ed.), Advances in child development and behavior vol. 10. New York: Academic Press (pp. 9-55).
Sigman, E., Goodenough, D. R., & Flannagan, M. (1979) Instructions, illusory self-tilt and the rod-and-frame test. Quarterly Journal of Experimental Psychology, 31, 155-165.
Smyth, M. M., Morris, P. E., Levy, P., & Ellis, A. W. (1987) Cognition in action. London: Lawrence Erlbaum.
Smyth, M. M. & Pendleton, L. R. (1989) Working memory for movements. Quarterly Journal of Experimental Psychology, 41A (2), 235-250.
Smyth, M. M., & Wing, A. M. (editors) (1984) The psychology of human movement. London: Academic Press.
Souder, M. A. (1972) Visual and proprioceptive determinants of space perception and movement. Journal of Motor Behavior, 4 (1), 13–22.
Squires, P. C. (1956) The shape of the normal work area. Report Number 275. Groton Connecticut: U. S. Naval Medical Research Laboratory.
Stelmach, G. E., & Larish, D. D. (1980) Egocentric referents in human limb orientation. In G. E. Stelmach and J. Requin (Eds.), Tutorials in motor behavior. Amsterdam: North-Holland (pp. 167-184).
Stevens, A., & Coupe, P. (1978) Distortions in judged spatial relations. Cognitive Psychology, 10, 422-437.
Strauss, W. L. (1974) The compete drawings of Albrecht Dürer. vol. 5. human proportions. New York: Abaris Books.
Sulcas, R. (1995) William Forsythe; Channels for the desire to dance. Dance Magazine, 69 (9; Sept.), 52-59.
Thorndyke, P. W. (1981) Distance estimation from cognitive maps. Cognitive Psychology, 13, 526-550.
Tolman, E. C. (1948) Cognitive maps in rats and men. The Psychological Review, 55 (4), 189–208.
Tulving, E. (1962) Subjective organization in free recall of ‘unrelated’ words. Psychological Review, 69 (4), 344-354.
Ullmann, L. (1966) Rudiments of space-movement. In R. Laban, Choreutics. Annotated and edited by L. Ullmann. London: MacDonald and Evans (pp. 138-210).
Ullmann, L. (1971) Some preparatory stages for the study of space harmony in art of movement. Surrey: Laban Movement Guild.
Viviani, P., & Terzuolo, C. A. (1980) Space-time invariance in learned motor patterns. In G. A. Stelmach and J. Requin (Eds.), Tutorials in motor behavior. Amsterdam: North Holland (pp. 525-533).
Wallace, S. A. (1977) The coding of location: A test of the target hypothesis. Journal of Motor Behavior, 9 (2), 157-169.
Wechsler, R. (1990) Symmetry in dance. Contact Quarterly 15 (Fall), 29–33.
Whiting, H. T. A. (1986) Toward a cognitive psychology of human movement. In B. Fleshman (Ed.), Theatrical movement: a bibliographical anthology. London: The Scarecrow Press (pp. 115–157).
Willott, J. F. (1973) Perceptual judgments with discrepant information from audition and proprioception. Perception & Psychophysics, 14 (3), 577-580.
Winearls, J. (1990) Choreography the art of the body. London: Dance Books.
Wing, A. M. (1980) The height of handwriting. Acta Psychologica, 46, 141–151.
Winter, D. D., Widell, C., Truitt, G., & George-Falvy, J. (1989) Empirical studies of posture-gesture mergers. Journal of Nonverbal Behavior, 13 (4), 207-223.
Witkin, H. A., Dyk, R. B., Faterson, H. F., Goodenough, D. R., & Karp, S. A. (1962) Psychological differentiation. New York: John Wiley.
Yates, F. A. (1966) The art of memory. London: Routledge and Kegan Paul. (Reprinted 1972.)