 |
|
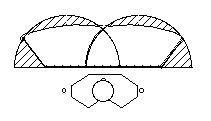
Figure IVA-18. The shape of the normal working area in the horizontal plane as semicircles or as prolate epicycloids (adapted from Squires, 1956, p. 2). |
The choreutic conception of deflected directions and the resultant kinespheric structure is very similar to measurements of body movements with the intention of designing efficient work spaces in ergonomic research. The most typical work space (see IIB.42) is the “normal working area” in the horizontal plane which is defined by the pathway of the hand as it sweeps across a table. Traditionally it was thought that the shape of the normal working area in the horizontal plane was semicircular, with the shoulder joint at the centre of the curve (Barnes, 1963, pp. 259-261; International, 1978, p.156). This assessment of a circular edge of the hand’s cumulative movement range appears to be the result of a simple prototypical sphere-like conception of the kinesphere (see IVA.21).
 |
|
Figure IVA-18. The shape of the normal working area in the horizontal plane as semicircles or as prolate epicycloids (adapted from Squires, 1956, p. 2). |
In contrast, Squires (1956) stated that “To portray the normal horizontal work area as a region consisting of two overlapping semicircular fields is misleading” and that “this portrayal has appeared persistently in the leading texts without exciting adverse critical comment” (p. 1). The articulations which occur when the hand traces a horizontal planar arc over a table-like surface were closely observed: Beginning by sitting with the forearm horizontal and the upper arm relatively vertical by the side of the torso, it was found that the elbow does not remain fixed, like a pivot-point for the arc of the hand. Rather, while the shoulder rotates outward (creating the arc of the hand) the shoulder also slightly circumducts (combined extension and abduction) creating a small arc of the elbow through space. These actions of shoulder rotation and shoulder circumduction occur simultaneously throughout the movement. Therefore, Squires (1956) found that the pathway of the hand which is “in harmony with naturalness, ease, and efficiency of human operation” is actually wider and flatter than a semicircle, in a curved shape identified to as a “prolate epicycloid” (Fig. IVA–18). Because of the limits of shoulder-joint rotation an angular peak occurred at the right-forward and left-forward directions. Similar results were found in Goel’s (1968) reassessment. The shapes of these curved hand paths correspond closely to the choreutic conception of a laterally deflected (rectangular-shaped) horizontal plane (see IVA.82).
Dempster and Colleagues (1959) measured the range of the hand’s pathway through a series of cycles in several parallel frontal planes which were combined into a single solid three-dimensional shape which they termed the “kinetosphere” (p. 291) (similar to a choreutic “kinesphere”, but that the hand maintains a single orientation throughout; see IIB.38). This solid shape was then sliced through its centre (kinetosphere centre, not body centre) in order to illustrate the shapes of the frontal, horizontal, and paramedial planes (pp. 303-310).
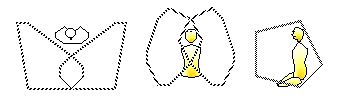 |
|
Figure IVA-19. Horizontal, frontal, and paramedial cross-sections |
Many similarities are evident between Dempster and Colleagues’ (1959) kinetospheric planes and the shape of the choreutic deflected kinespheric planes (see Fig. IVA-19). While the edges of the planes are generally curved, corners can be identified by the presence of obvious curvature peaks. When the kinetospheres of both arms are combined then four peaks are evident within a horizontal cross section which roughly corresponds with the four corners of the choreutic (laterally deflected) rectangular-shaped horizontal plane (with “wings” stretching to the right-backward and left-backward directions). The frontal planar cross sections are in the shape of “narrow vertical ellipses” (p. 298) with their peaks above and below the shoulder joint (and slightly wider), thus creating a vertically oriented rectangular plane similar in shape to the choreutic (vertically deflected) frontal plane. The paramedial planar sections contained peaks which correspond to the up-forward and down-forward corners of the choreutic (sagittally deflected) medial plane.
Other attributes of Dempster and Colleagues’ (1959) kinetospheres are also similar to the hypothesized shape of the choreutic kinesphere. For example, the “maximum contour” (p. 306) which passes through the up-forward and down-forward peaks of the paramedial plane and also through the right-backward (or left-backward) peak (ie. the “wing”) of the horizontal plane has a remarkable similarity to choreutic pentagon-shaped “5-rings” which are in this same orientation (Preston-Dunlop, 1984, pp. 81; see IVA.83).
Many differences are also evident between Dempster and Colleagues’ (1959) kinetospheres and the hypothesized deflected shape of the choreutic kinesphere. The kinetospheres rarely extended very far behind the mid-frontal plane of the body nor did they extend far below the waist. This occurred for the kinetospheres because of the constraints imposed on the body movement for the sake of obtaining precise measurements. The torso was held immobile which limited the range of motion downwards and backwards. An apparatus was also held in the hand which required the orientation of the hand to be fixed throughout the movement (eg. the palm always facing forward). With this constraint on hand orientation the limits of wrist articulation severely restrict the extent to which the hand can reach behind the body.
A prototype/deflection hypothesis was identified in choreutics which posits that kinespheric dimensional and diagonal orientations serve as idealised conceptual prototypes of pure stability and pure mobility, while actual bodily movements occur as deflections (“inclinations”) between nearby dimensional and diagonal directions.
Similar spatial prototypes are evident in the English language where dimensions are given the greatest conceptual specificity, diagonals (45°) are given less, and off–diagonal inclines are given the least specificity. Prototype effects are also demonstrated in spatial cognition research where (for example) dimensional orientations are perceived and responded to more readily than diagonal orientations (“oblique effect”) and lines or angles are perceived/remembered to be more dimensional, or to be closer to 90°, than they actually are.
Anatomical constraints are identified as a principal source of deflections. Measurements of ranges of motion at single-joints did not support the deflection hypothesis but these are not ecologically valid measures of whole-body kinespheric structure. Kinesiological analyses of joint structures and muscular lines-of-pull both supported the hypothesis that body movements tend to move out of pure dimensionally-oriented Cartesian planes and into obliquely tilting paths. Therefore, oblique directions must be considered to be kinesiologically simpler than dimensional and Cartesian planar paths.
Deflections are described in choreutics as arising from many sources including; rotary joint articulations which take the motion out of a pure Cartesian plane; effects arising from the physical forces generated during a movement (eg. momentum): and also from the desire by the mover to produce a particular expression or communication. The physical forces and expressive qualities of moving within Cartesian planes are flat, rigid, and contained, compared with the physics and expression of movement along inclined planes. Laban (1951, p. 11) made a similar observation that the inclinations are “most obvious in the expressions of emotional excitement” when the dynamism of inclinational slopes would be overtly exhibited.
The hypothesised deflected inclinations create an icosahedral-shaped kinespheric structure with rectangular-shaped Cartesian planes. This is remarkably similar to ergonomic measurements of the shape of the workspace or “kinetosphere”.
The choreutic conception can be considered to be a counter-part to the ballet conception. Ballet is based on a conception of dimensions which are implicitly deflected towards nearby diagonals during actual body movement. In contrast to this, choreutics is based on a conception of diagonals which are explicitly deflected towards nearby dimensions during actual body movement. Laban (1926, p. 64) summarises that ballet is “oriented in dimensional stability” while the “new dance” is “oriented in diagonal lability” and so Laban used the choreutic diagonal scale as the principal exercise in his dance technique classes (Bodmer and Huxley, 1982, p. 18). A few examples of ballet movements deflecting into inclinations are given here. The further development of a choreutic diagonally-based para-ballet movement technique is possible with an understanding of organic deflections into inclinational directions. This is a direction for future research.