 |
|
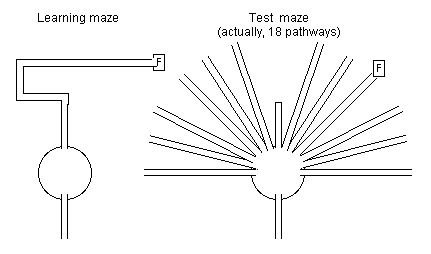
Figure IIIC-1. Tolman’s rat maze; learning maze and test maze; F = food box (adapted from Tolman, 1948, pp. 202-203; Tolman et al., 1946, pp. 16-17). |
After individual locations are well learned they are typically linked together and mentally represented within a map-like image. This identification of cognitive maps in psychology validates the map-like conceptions of the kinesphere used in art, architecture and in Laban’s unique method of using polyhedral-shaped cognitive maps of the kinesphere in choreutics.
“Cognitive maps” are often considered synonymous with “spatial representations” (Kosslyn et al., 1974, p. 708). This refers to the “representation of information from a geographic area that cannot be perceived simultaneously” (Allen et al., 1978, p. 617) and is “picture-like, that is, embodied in a visual image much like a map” so that during spatial tasks Subjects report that they “formed a picture of the path” and recall consists of “searching for the correct picture” (Levine et al., 1982, pp. 160, 166). “Cognitive mapping generally refers to the process by which individuals collect, organize, store, retrieve, and manipulate information concerning location in space” (Sadalla et al., 1979, p. 291). Thus, Neisser (1976, p. 111, 118, 123-125) uses “‘orienting schema’ as a synonym for ‘cognitive map’” since the representation will accept sensory information about a particular environment and also direct further bodily movements within that environment. “Mental images” or “spatial imagery” are considered to be aspects of this orienting schema.
Tolman’s (1948) classic article reviews work with Students and Colleagues on experiments in which Subjects (mostly rats) must find a path through a maze toward a reward (food). In the typical maze-learning behaviour a hungry rat will gradually learn her way through a maze so that each successive trial will be faster and have less errors (wrong turns) than previous trials. Two theories are proposed to account for this behaviour (pp. 189-193): 1) The rats learned a stimulus-response chain in which each action serves as the stimulus for the next action (eg. turn right, go forward, turn left); or 2) That the rats learn a “field map” or a “cognitive-map of the environment” in which the entire environment is laid out in the rat’s mind as a map-like spatial image. These two possibilities might also be described as 1) “route learning” or “associative learning” versus 2) learning a “cognitive map” or “survey map” (Levine et al., 1982, p. 160).
IIIC.11 Equiavailable, Path Free, Spatial Knowledge.
Levine and Colleagues (1982) state the “cognitive-map hypothesis” and the “principle of equiavailability” in three axioms:
AXIOM 1: From a sequence of movements in space, one is able to construct a representation (eg. a picture) of the path. . . . that people have the ability to convert a limited degree of sequentially obtained spatial information into a simultaneous system. . . .
AXIOM 2: From a picture of a path, one can move appropriately among the points of the path itself. . . . the information is presented simultaneously to the Subject, who reads it out into a sequence of movements. . . .
AXIOM 3: After learning a sequence of connected points, humans behave as through the information has been placed into a simultaneous system. That is, they behave as through they have a picture available. . . .
(Levine et al., 1982, pp. 160-161)
The implications for experimental research are that Subjects should be able to execute paths which have never before been experienced (shortcuts). These “new” paths and the “old” paths should be “equally available” within this picture-like or map-like image .
Tolman (1948, p. 193) also distinguishes between the path-specificity of maps. If the mental maps are “relatively narrow and strip-like” then only the particular paths experienced during learning will be encoded into this “strip-map” (path-specific). If the mental maps are “relatively broad and comprehensive” then the rat has derived the structure of the overall environmental layout from her experiences of individual paths. In this case the rat would still know the correct overall direction to travel towards the food even if some of the intermediary paths changed (path free).
Similarly Moar and Charleton (1982, p. 382) distinguish between different hypotheses: The “route hypothesis” posits that “schemata based on individual routes are an essential unit or representation in our acquisition of cognitive maps” versus the “network hypothesis” which posits that “if two or more different routes have to be learned, and if the routes intersect in an obvious manner, then schemata based on a network of these routes may be used”. These are closely associated with the “sequential hypothesis” which posits that “when we initially learn a route, we build up a linear sequence of associations containing information only about the serial order of the landmarks and the direction of turns” versus the “spatial-map hypothesis” which posits that “the route would be functionally represented as a series of landmarks on a map”.
Tolman (1948, p. 203) reports that equiavailability is often noted when rats who have learned a maze crawl out of the starting box onto the top of the maze and run directly to the location of the food-box. This indicates that the rats have knowledge of the location of the food which is independent of the particular maze paths which they had experienced. Similar results are reported for monkeys who move directly towards food regardless of the pathways through which they had experienced the locations of the food (Neisser, 1976, p. 118).
 |
|
Figure IIIC-1. Tolman’s rat maze; learning maze and test maze; F = food box (adapted from Tolman, 1948, pp. 202-203; Tolman et al., 1946, pp. 16-17). |
Tolman (1948, pp. 202-204) also reports on previously published work (Tolman et al., 1946) in which rats began by thoroughly learning a maze which crossed a large circular table, then went down a tunnel through a roundabout path ending at a food-box. Next, a semi-circle of radiating tunnels was added around the circular table and the old path was blocked (Fig. IIIC-1). After the rats realised the old path was blocked they explored the other options and the majority of rats chose to go all the way down the path that led most directly to the location of the food box. Thus the rats had learned the direction to the food independently of the path used to get there.
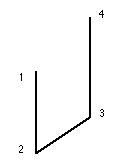
Levine and Colleagues (1982) experimented with two types of space. In the “tabletop-terrain” the arm-hand-finger movement occurred within a paper-sized space (81/2 x 11 inches) and in the “floor terrain” Subjects walked within a small room (32 x 50 feet). In both cases blindfolded Subjects were guided through a “four point path” (eg. three path segments joining points 1-to-2, points 2-to-3, and points 3-to-4) (Fig. IIIC-2) and then were tested on their ability to execute four different types of paths: 1) A “simple forward movement” consisted of a repeat of a previously experienced path (eg. points 1-to-2, 2-to-3, or 3-to-4); 2) A “simple reverse movement” consisted of a previously experienced path executed in retrograde (eg. points 2-to-1, 3-to-2, or 4-to-3); 3) A forward direction “shortcut” consisted of a “new” movement in the forward order (eg. points 1-to-3, 1-to-4, or 2-to-4) and; 4) A reverse direction “shortcut” consisted of a “new”movement in the retrograde order (eg. points 4-to-3, 4-to-1, or 3-to-1). Results showed that accuracy was equivalent regardless of which type of path was being performed. This supports the principal of equiavailability in a path-free map-like spatial representation. This also occurred regardless of various transformations (or not) required between learning and recall (see IIID), these included: 1) Learning and recalling the tabletop terrain with the same arm; 2) Learning the tabletop terrain with one arm and recalling it with the other arm; 3) Learning from a visual picture and recalling with an arm in the tabletop terrain; 4) Learning and recalling in the floor terrain by walking. These transformations indicate that recalling spatial locations is not dependent on the particular muscles used during learning and so supports the use of an abstract spatial location code (see IIIB).
 |
|
Figure IIIC-2. Four point path followed with arm movements or walking (Levine et al., 1982). |
Many researchers have probed cognitive maps by using photographic-slides depicting several scenes along a walk. This slide-show stimuli is an impoverished form of the actual perceptual experience which the Subjects would have if they actually took the walk. Even with this degree of sensory impoverishment a map-like image of the overall spatial layout is developed in Subjects’ memories.
Moar and Carleton (1982) showed Subjects one slide for every eight meters of two different intersecting paths (240 meters for each walk) through an unfamiliar city area. Subjects then drew lines on paper the appropriate length and direction to judge the distance or direction between two loci in the paths. Judgments were proportionately accurate regardless of whether the two loci were in the same or different paths. This supports the hypothesis that individual paths are integrated into an overall network rather than remaining separate.
Moar and Carleton (1982) also found that after initial viewing of the slides judgments of distance or direction along the normal order of the route were proportionally more accurate than judgments along the retrograde route order. However after viewing the slides four times this difference disappeared. This indicates that during initial acquisition the spatial representation is based on the path-specific “sequential associations” within certain routes but with further learning the spatial representation becomes more map-like and path-free (p. 392). Likewise, learning environments by walking initially creates knowledge only of the particular paths experienced, but with more learning these are integrated into map-like, path-free knowledge (Moar, 1978; Thorndyke and Hayes-Roth, 1982).
IIIC.12 Locations, Landmarks, Reference Points.
Particular locations are identified in the spatial environment which are used as “landmarks”. These might consist of distinct features along a route which assist in navigation, distinct features within a region which assist in maintaining orientation, or the most easily recognised features from a particular environment.
Allen and Colleagues (1978) showed Subjects a series of thirty slides of a 360 meter path in either the normal or a random order. Regardless of the presentation order Subjects could distinguish other slides from a different walk but could not distinguish between the slides which had been seen and other slides (not previously seen) of the same walk. Distance judgments between landmarks along the walk were also in proportion to real-word distances. This indicates that Subjects “‘fused’” the slides into an “integrated context” (p. 621) which “can be attributed to their ability to extract information from the perceptual overlap between scenes” (p. 624). That is, if a landmark (eg. a tall building) appeared in two different slides it could be used to link those scenes together. The overall map-like image of the space appeared to be developed by linking together the various landmarks into a network, regardless of the particular pathways. This use of landmarks as the basis of cognitive maps was further supported since distance judgments between slides rated as “high landmark potential” were more accurate than between slides with “low landmark potential”.
Sadalla and Colleagues (1980) distinguish these landmarks from “reference points” which are special landmarks used as prototypical loci so that “the position of a large set of (nonreference) locations in a particular region is defined in terms of the position of a smaller set of reference locations” (p. 516). They found that certain locations in a university campus or small city appear to be used as cognitive reference points in that they are judged to be farther from another location than vice versa. This approach of probing for asymmetric distance judgements was developed earlier by Rosch (1975a) and is used in this research to probe whether reference points are used in cognitive maps of the kinesphere (see IVA.110).
IIIC.13 Hierarchy of Map-like Spaces.
IIIC.13a Higher-order regions and borders.
Spatial environments appear to be segmented into higher-order regions separated by borders. These are indicated in various ways, including the speed of direction judgements, and when the judged distance or direction between two locations is biased towards the distance or direction between the higher-order regions.
Wilton (1979) asked Subjects whether one town is in a particular direction (eg. north) from another town. When the two towns were far apart, or were nearby but within separate regions (ie. two different countries) the direction judgment was made quickly. Wilton reasons that the relations between towns cannot be represented as strings of connections between neighboring towns since this would require a longer time to verify the overall direction between distant towns. The alternative explanation is that fast judgments are made between towns which are in different high-order regions (eg. different countries) because this can be determined by consulting a high-order “coarsely graded” mental map, whereas cities within the same region require longer time for the direction judgment because a lower-order “finely graded” mental map must be inspected.
Similarly, Lehtiö and Colleagues’ (1980) Subjects imagined they were standing at a location in a well known city and judged whether another location in the city was to the right or left of their imagined line of sight. Reaction times to make the direction judgment were quicker when the distance between the two locations was more distant, or when self-rated familiarity with the locations was greater. They interpreted this as indicating a hierarchical structure with different “degrees of resolution” at the different levels. In the higher-order “fuzzy” mental map distant and well known locations can be quickly compared while more specific information must be retrieved from a lower-order “detailed” map.
Stevens and Coupe’s (1978) Subjects imagined a city at the centre of a circle (with north indicated) and drew a line from the centre of the circle towards the judged location of another city. The direction judgments between cities tended to align with the directions between the higher-order regions (eg. states or countries). Similar results were also obtained after studying page-sized (21 x 21 cm) maps of imaginary environments. Therefore it appears that directions between real or imaginary cities were remembered according to the directions between their higher-order regions.
McNamara (1986) found three types of effects indicative of the space being divided into higher-order regions. They used a room-sized (20 x 24 feet) or a page-sized (8.5 x 11 inches) space containing four borders and thirty-two objects (or names of objects). In a recognition task an object was recognised faster when it was preceded (primed) by an object within the same region. Direction judgments between two objects tended to align with the direction between the two higher-order regions. And distance judgments were overestimated between two nearby objects when they were in different higher-order regions.
Hirtle and Jonides’ (1985) Subjects recalled thirty-two locations from the centre of a city with no “strict boundaries” between regions. Nonetheless, higher-order regions were identified within the spontaneous groupings in Subjects’ recall orders; locations within the same subjective region were recalled in the same cluster and these groupings did not change in a test six weeks later. Distances between two locations were judged to be larger when they were in different subjective regions and judged to be smaller when they were in the same Subjective region. These hierarchical effects occur even in a space with no obvious regions.
Allen and Kirasic’s (1985) Subjects viewed 60 slides of a 1000 meter walk through a residential area and were asked to divide the route into segments, or “what appeared to them to be a new part of the walk” (p. 219). Five segments were distinguished. Other Subjects (who had not consciously divided the path into segments) then made distance judgments and it was found that when locations were in different higher-order regions they were judged to be further apart. Thus, the hierarchical effect occurred regardless of whether Subjects intended to divide the space into regions.
McNamara and Colleagues (1989) looked for hierarchical effects in spaces least likely to produce it. Subjects learned the locations of twenty-six objects (eg. coin, shoe, egg) randomly distributed throughout a room-sized (20 x 22 feet) or a page-sized space. Subjective regions were identified according to the repeated grouping of objects into clusters during their free recall. The use of these subjective regions was confirmed by priming effects (an object is recognised faster if the preceding object was from the same region) and because distance judgments were biased by the higher-order region (distance between objects is judged smaller if they are in the same region). Again, a hierarchical structure was evident in the spatial representation even in the absence of any obvious higher-order regions in the space. They propose that the hierarchy emerges as a strategy to increase memory capacity by grouping information in to “chunks” (eg. Ericsson et al., 1980) or “clusters” (eg. Miller, 1956; see IVB.51) and that these spatial clusters become higher-order regions.
Kosslyn and Colleagues (1974) used children (4-5 years) and adults who learned the locations of 10 toys in a room-sized space (17 x 17 feet) by walking in the space and placing or removing toys from their designated locations. Movement was restricted to walking directly to the toy’s location and back to “home base”, and by four barriers which divided the space into quadrants. Two barriers blocked vision (opaque) and two did not (transparent). Results indicated that distance judgements were bias toward the distances between regions (two objects in different regions were judged as more distant than two objects in the same region, regardless of their actual distance). A developmental process was also indicated in which children tended to separate the space into four regions (with both types of barriers as boundaries) while adults tended to separate the space into two regions (opaque barriers only) (duplicated by Newcombe and Liben, 1982).
IIIC.13b Continuity of spatial extensions.
In addition to different sized regions, the notion of cognitive maps has also been used for different sized spaces (from the size of a piece of paper to the size of Earth). Similar learning and recall effects typically occur regardless of the size of space studied which indicates that there is a continuity of representation across sizes of spatial extensions. The notion of cognitive maps is equally applicable to all sizes of space from geographical directions to directions of limb movement.
The notion of “cognitive maps” typically refers to “the acquisition and use of spatial knowledge of large-scale environments”, and thus “macrospatial cognition” (Allen and Kirasic, 1985, p. 218), or to a “large-scale spatial image” while the space of a small object or the size of a table-top are considered to be “microspaces” (Hardwick et al., 1976, pp. 1, 3). However, in other cases “cognitive maps” refer to spatial representations of any sizes of “environments committed to memory” (Hintzman et al., 1981, p. 155), including buildings within a city, objects in a room, drawings on a piece of paper, or directions of body parts. Ability for spatial orientation is considered to be a behavior which ranges from large-scale “geographical orientation” through to small-scale “limb orientation” (Stelmach and Larish, 1980, p. 168). “Space perception” is considered to range from “detection of a stable framework of the environment” through to “finer manipulative movements of skill” (Souder, 1972, p. 14). Likewise, Siegel and White (1975, p. 13) consider that “fundamental concepts” of space (eg. reaching toward directions, manipulating objects, locomotion) and “macrospatial cognition” (eg. knowledge of large-scale routes and loci) “are not independent - they are merely two aspects of the same generic problem” within spatial cognition.
Neisser (1976, pp. 113, 123) describes how “a cognitive map is essentially a perceptual schema” and thus is similar to other spatial representations (eg. of solid objects) in that large-scale environments are encoded into memory in a way very similarly to small-scale objects. Indeed, directions and movements of body parts are at the basis of knowledge of cognitive maps of any sized space since they are used during the actual physical process of spatial learning and recall (see IIC.33). For example Hochberg (1975) recorded eye movements and observed that when Subjects observe a small-scale object it is subdivided into several landmarks that receive the most repeated fixations. That is, an observer gathers information about large-scale and small-scale terrains in a similar way, by guiding locomotor movements in a large-scale space, and by guiding eye and limb movements in a small-scale space.
The spaces studied are freely varied from small-scale to large-scale spaces. Stevens and Coupe’s (1978, Ex. 3) “map” of an imaginary country was a page-sized space which was learned by visual inspection. Recall of directions between map loci was then made by drawing appropriately oriented lines on paper. This task was considered to be analogous to cognition about a large scale environment but in practice it takes place entirely within the Subject’s kinesphere. Likewise, Thorndyke’s (1981) Subjects learned a map by drawing it. In these cases a large-scale environment is learned through vision and kinesthesia in a small-scale space within reach of the limbs. McNamara and Colleagues (1989, Ex. 2) refer to a page-sized array of thirty-two object names (eg. fan, candy, soap, shoe) as a “map” of the locations of the objects. Two ranges of space are used for the “map”; the locations within a room-sized space experienced by walking (placing the objects at their correct location), and the locations within a page-sized space experienced by eye and arm movements (placing the names at the correct location).
Levine and Colleagues’ (1982) Subjects undertook the same groups of tasks in a “tabletop terrain” (experienced with arm/hand movements) and a “floor terrain” (experienced with locomotion). Similarly, Presson and Hazelrigg’s (1984) Subjects learned about an environment by walking along a floor path or looking at a (50 x 50cm) map. In all cases spatial recall effects were identical regardless of the size of the space used.
Hintzman and Colleagues (1981) refer to a small circular area (6cm) as a “visual map” (p. 155), the remembered locations of objects in a tiny (1.6 x 1.6 m) room as a “cognitive map” (p. 162), and the perception of points touched on one’s head as a “tactile map” (p. 175). In all cases the information in the “maps” is recalled by the direction of an arm movement through a small (9 cm) diameter circle. Recall effects are similar regardless of the size of the space.
Likewise, the “symbolic distance effect”* was found to occur for distance judgements about buildings on a campus (learned by locomotion) and for states of the U. S. A. (learned from maps) (Evans and Pezdek, 1980). This indicates that map learning and locomotion learning lead to a similar type of spatial memory representation.
__________
* The closer in length are two distances (or sizes), the longer time is required to determine which distance (or size) is larger.
__________
Many researchers also refer to “mapping” processes within body movement perception and recognition of small-scale objects. Paillard and Brouchon (1974, p. 283) discuss how kinesthetic “position cues have a real function of ‘marking’ space . . . [within] some internal map necessary for the elaboration of a complex program of spatially coordinated motor activities”. Saltzman (1979, p. 113) refers to the “task-space mapping” of limb movements within the workspace. Heister and Colleagues (1990) refer to perceptions of external space according to the relation with anatomical locations as “spatio-anatomical mapping”. Humphreys (1983, p. 151) discusses how recognition of objects is achieved by “mapping” the sensory information into a memory representation. Ruff and Perret (1982) refer to a “spatial mapping” process by which a form is derived by auditory tracking the pathway of an unseen sound source. This indicates how many spatial ranges and activities can be considered to consist of “mapping”.
Studies in the choreutic tradition also use an analogy in which polyhedra “are like maps” and the paths of movement are like “specific routes” along the map (Bartenieff and Lewis, 1980, p. 29). Laban (1926) describes how “we must construct particular points around us”, that paths are created by connecting “point to point” (pp. 21-22), and that these are used as “orientation points” for the mapping of the path (p. 11). A “choreutic map” is used for “mapping choreutic configurations” (Salter, 1983, p. 166), and the three Cartesian planes can be used as “points of reference” in order to undertake a “mapping” of body movements (Moore, 1982, pp. 68–69).
In summary, there appears to be a continuity of spatial representation ranging along a continuum from small spaces (explored and learned via limb movement) nested within large spaces (explored and learned via locomotion). Map-like images have similar cognitive characteristics regardless of the size of the space.
The bodily reach space, work space, or “kinesphere” (see IIB.38) has been conceptualised as a map-like image by artists, architects and within choreutics. The image of the kinesphere might be referred to as a map, grid, graph, network, framework, scaffolding, or a lattice. These terms express the same general idea in slightly different ways.
Body movements are often considered to be organised into a mental representation analogous to a map within choreutics and motor control research (see IIIC.13b). A “map” is essentially defined as a diagrammatic representation of anything:
a diagrammatic representation of the . . . geographical distributions, positions, etc., of natural or artificial features such as roads, towns, relief, rainfall, etc., . . . a diagrammatic representation of the distribution of stars or of the surface of a celestial body . . . a map-like drawing of anything. (Collins, 1986).
Laban (1966, pp. 68, 101-107) uses the analogy of the kinespheric structure as a “scaffolding” which can be defined as “a temporary metal or wooden framework that is used to support workmen and materials during the erection, repair, etc., of a building or other construction” (Collins, 1986). This emphasizes Laban’s architectural analogy evident in many places, for example the famous statement that “Movement is, so to speak, living architecture” (Laban, 1966, p. 5), the referral to movement as being a “‘building process’” (Laban quoted by North, 1972, p. 9), the conception that movements are “constructed” (Laban, 1926, pp. 28, 88 [“gebildet”]), and so “we must construct particular points [of the kinesphere] around us” (Laban, 1926, pp. 21-22). Laban (1966, p. 124) regards the scaffolding much like a map in that “trace-forms following the simple lines of the scaffolding can be represented mentally without great difficulty”.
Bernstein (1984, p. 109) refers to the spatial organisation of body movements as the “co-ordinational net of the motor field”. Networks consist of “a number of parts, passages, lines, or routes that cross, branch out, or interconnect” (American, 1982) and are used in a variety of applications such as analysing railroad tracks and airline routes (Frank and Frisch, 1970). The network analogy emphasizes the flow of motion along “links” in the net from locus to locus.
The kinespheric structure is sometimes considered to be analogous to a “grid” in choreutics (Preston-Dunlop, 1984, p. 17) and in architecture (Le Corbusier, 1980, pp. 37-44). The grid analogy emphasizes a regular “pattern of horizontal and vertical lines . . . used as a reference for locating points” (American, 1982), for example the pattern of latitude and longitude lines on the map of the earth.
The term “lattice” is used to refer to the regular pattern of molecular arrangement in crystals or as decorative landscaping woodwork. It is defined as an “open framework made of strips of metal, wood, or similar material interwoven to form a regular pattern . . . [and] A regular, periodic configuration of points, particles, or objects throughout an area of space, esp. the arrangement of ions or molecules in a crystalline solid” (American 1982). This is similar to the choreutic conception of polyhedral structures of the kinesphere.
Kinespheric structures could also be referred to as “graphs” which are defined as “depicting the relation between certain . . . quantities by means of a series of dots, lines, etc., plotted with reference to a set of axes” (Collins, 1986). Choreutics uses polyhedra which can be considered to be “platonic graphs” (Wilson and Watkins, 1990, p. 38) when each node of the graph is located at each polyhedral vertex.
In summary, each term has a slightly different emphasis. The most general term is a “framework”, defined as “a structure or frame supporting or containing something” (Collins, 1986). “Scaffolding” emphasizes Laban’s architectural metaphor. “Grid” or “graph” emphasize the loci and reference lines used in maps to specify particular loci. “Map” emphasizes the identification of loci and paths of various kinespheric forms. “Lattice” emphasizes the polyhedral crystalline structure. “Network” or “net” (following Bernstein, 1984, p. 109) is used here since it is descriptive of the linking together of multiple loci in any formation. The choice of a term is somewhat arbitrary. “Scaffolding”, “grid”, “graph” and “lattice” may indicate a fixed, stable kinespheric structure, whereas the notion of a net is more pliable and lends itself nicely to conceptions kinespheric forms deflecting across variously shaped polyhedral nets (see IVA.80; IVB.34).
IIIC.31 Cartesian Coordinates and Planes.
The most common kinespheric network consists of the “x”, “y”, and “z” axes of the Cartesian coordinate system and the corresponding three “Cartesian planes” (“xy” plane, “yz” plane, “zx” plane) which are used in anatomy and kinesiology to specify the locations and movements of body-parts (Kapit and Elson, 1977, p. 1; Rasch and Burke, 1978, p. 97; Wells and Luttgens, 1976, p. 21). The three dimensions and three planes have been referred to with various terms (see Appendix VIII). In this study the following terms will be used:
| Planes: | |
| Medial | (or paramedial to specify a non-central plane) |
| Frontal | (or midfrontal to specify a central plane) |
| Horizontal | (or midhorizontal to specify a central plane) |
| Dimensions: | |
| Vertical | (up/down) |
| Sagittal | (forward/back) |
| Lateral | (right/left) |
 |
|
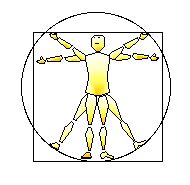
Figure IIIC-3. Proportions of the human figure (adapted from Leonardo Da Vinci’s drawing; Heydenreich, 1928, p. 10; Strauss, 1974, p. 2475). |
IIIC.33 Planar Networks.
The kinesphere is often partitioned by representing it as variously shaped planar networks. Much of this has been with the intention of defining the proportions of the human body. The most famous example is probably Leonardo Da Vinci’s “sketch showing the proportions of the human figure” (Heydenreich, 1928, p. 110; also in Strauss, 1974, p. 2475) in which the body is presented within a square-shaped frontal plane and circumscribed by a circle (Fig. IIIC-3). Doczi (1981, p. 93) reports that this conception originated from earlier books on architecture published by the Roman Marcus Vitruvius Pollio.
The Renaissance painter Albrecht Dürer (eg. Strauss, 1974) also aligned a circle and square with the body’s frontal plane (p. 2426), experimented with conceptions of the human chest as a frontal pentagon-shaped plane (p. 2465), and placed the entire body or various body-parts within square and rectangle nets in the frontal or medial planes (pp. 2476-2477). Similarly, Doczi (1981, pp. 96-100, 143) and Ghyka (1977, pp. 97–109) lay various frontal planar networks of squares, rectangles, and circles over the entire body or individual body-parts in an analysis of body proportions and directions of movement.
 |
|
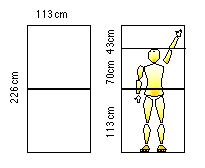
Figure IIIC-4. Grid of proportions (adapted from Le Corbusier, 1980, p. 66). |
The architect and painter known as Le Corbusier (1980 pp. 37-44, 53–58) describes the process of deriving a “‘grid of proportions’” which is “designed to fit the man placed within it” (p. 37) and so “mathematical order is adapted to the human stature” (p. 41). This grid was intended to provide a body-scaled system of measurement which “should be set above both the system of the foot-and-inch and the metric system” (p. 45):
. . . a “grid of proportions” . . . will serve as a rule . . . a norm offering an endless series of different combinations and proportions; the mason, the carpenter, the joiner will consult it whenever they have to choose the measures for their work; and all the things they make . . . will be united in harmony. That is my dream. (Le Corbusier, 1980, p. 37)
Le Corbusier’s (1980) kinespheric net is oriented in the frontal plane and is based on two squares forming a rectangle (226 cm high, 113 cm wide) (p. 66) based on the average height of a human of six feet (182.88 cm) (p. 56). Within this basic network many other relations are constructed, including right angles, the golden proportion, and measurements corresponding to the Fibonacci series (Fig. IIIC-4).
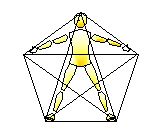
Laban (1966) briefly discusses planar arrangements of poses in which the body has a “two-dimensional feeling . . . resembling the plane-like formation of the leaves of plants” (p. 18). One of these typical poses creates a pentagon/pentagram-shaped planar network (Fig. IIIC-5) which is described as an “elementary posture” in which “Our flat bodily structure encourages a division into five principal zones: the zone of the head, the two zones of the arms, and the two zones of the legs” and is “like a star with five equal pulls towards five points of the kinesphere” (pp. 19-20 [also pictured by Bartenieff and Lewis, 1980, p. 113]). Laban conceives of this pentagon pose as possibly transforming into a quadrangle pose (Fig. IIIC-6):
Sometimes an awareness of the extended arms and legs prevails, when the arms are somewhat raised and tension is particularly stressed in the extremities. We then becomes less conscious of the vertical direction [in the pentagon pose], but have rather the feeling of a quadrangular construction. This tension tends to evoke a more ecstatic feeling than that [“intellectual awareness”] accompanying the pentagonal attitude. (Laban, 1966, p. 20)
 |
|
Figure IIIC-5. Pentagonal body pose (adapted from Laban, 1966, p. 19). |
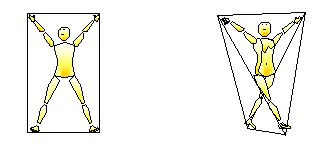
Quadrangle poses are conceived to transform further into tetrahedral poses when the arms and legs are no longer within the same plane (Fig. IIIC–7). These are described as “plastic variations of the flat quadrangle (Laban, 1966, pp. 20-21) or as “tetrahedral tensions” (Bartenieff and Lewis, 1980, pp. 97–99). Laban (1984) made many drawings of variously shaped tetrahedral nets for different body poses.
 |
|
|
Figure IIIC-6. Planar quadrangle network . |
Figure IIIC-7. Tetrahedral network (adapted from Laban, 1984, p. 18). |
The five regular polyhedra* are principally used which are representative of the most equalised, symmetrical divisions of three-dimensional space.# Occasionally other irregular polyhedra are also used (see below). The possibilities for polyhedral nets are endless, for example Wenninger (1971) presents over one-hundred varieties and states that this includes “only some polyhedral forms . . . [with] obvious omissions” (p. 204). However, the vast majority of the irregular polyhedra are themselves derived from the five regular polyhedra (via operations such as truncation, stellation, and interpenetration; see Holden, 1971), and so the five regular polyhedra can be considered to be higher-order networks while the other irregular polyhedra are lower-order variations. These polyhedral nets are briefly mentioned here and are considered in more detail later (see IVA.20).
__________
* A “regular” polyhedron contains all edges of equal length, all angles of equal degree, and all polygonal surfaces of identical shape. The five regular polyhedra (also called “platonic solids” since they are mentioned in Plato’s Timaeus) are the tetrahedron (four triangle surfaces, four vertices), hexahedron (ie. cube; six square surfaces, eight vertices), octahedron (eight triangle surfaces, six vertices), dodecahedron (twelve pentagon surfaces, twenty vertices) and the icosahedron (twenty triangle surfaces, twelve vertices) (For discussion of polyhedra, truncations, etc. see Holden, 1971).
# Whereas an infinite number of regular polygons divide two-dimensional space into equal parts (eg. triangle, square, pentagon, heptagon, octagon, etc.), only five regular polyhedra are possible which divide three-dimensional space into equal parts.
__________
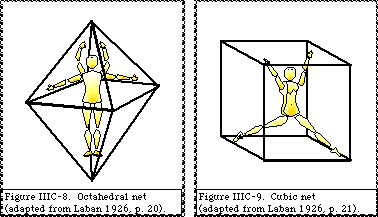
IIIC.34a Octahedron and cubic nets.
The dimensional directions are joined to build an octahedral network (Fig. IIIC–8). The diagonal directions are joined to build a cubic (hexahedral) network (Fig. IIIC-9). Many variations of the cubic net are used. Laban (1966, pp. 12-71, 95–99) represents kinespheric forms on a net of three parallel horizontal planes or “three levels in cubic space” (p. 16) which correspond to a higher-order cubic-shaped network. A cubeoctahedral network is also used (p. 104) which can be derived from the cube or the octahedron by connecting the mid–points of their edges. Occasionally a rhombic dodecahedron is used (Laban, 1984, p. 66) which is derived by linking the
six vertices of the octahedron together with the eight vertices of an interpenetrated cube. Cubic nets have also been used as a “space module” for the conceptual representation of ballet positions and movements (Kirstein and Stuart, 1952, pp. 2, 20, 30).
IIIC.34b Icosahedral and Dodecahedral nets.
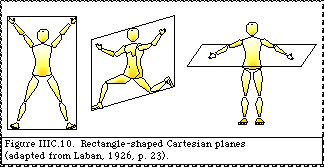
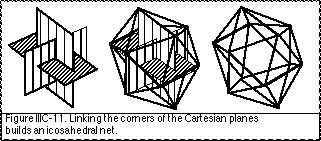
The corners of the three Cartesian planes are joined together to create variously-shaped networks. The hypothesised shape of the Cartesian planes is one aspect of the choreutic prototype/deflection hypothesis (see IVA.24). When the Cartesian planes are square-shaped (ratio between sides 1 : 1) then their corners can be joined into a twelve-loci cubeoctahedral net which is a variation of the octahedral or cubic net. If the Cartesian planes are rectangle-shaped with the proportion of the “golden section” (ratio between sides ‰ 1.618 : 1) (Fig. IIIC-10) then their corners can be joined into a twelve-loci icosahedral net (Fig. IIIC-11) (Laban, 1926, p. 23; Ullmann, 1966, p. 142). If the Cartesian planes are shaped in long narrow rectangles (ratio between sides ‰ 2.618 : 1) then they can be linked together with the eight diagonal directions into a twenty-loci dodecahedral net.
The actual shape of the kinespheric net during certain movements has been measured by ergonomic and motor control researchers (eg. Dempster et al., 1959). This is considered in more detail within the discussion of the choreutic prototype/ deflection hypothesis (see IVA.90).
In an anthropometric and ergonomic study, Critchlow and Robinson (1962; Critchlow, 1969, pp. 86-89) used Laban’s work as their basis and developed a kinespheric network consisting of a truncated octahedron containing a truncated icosahedron. Since each point of the octahedral or icosahedral net had been truncated (ie. cut off) a small polygonal surface remained where each vertex used to be. This can be conceived of as expanding the area of each locus so that each single locus is now surrounded by a small polygonal network of locations.
IIIC.34c Tetrahedral net.
A tetrahedral network is used in choreutics as an underlying basic or elemental net. Laban (1966) considers that “almost all positions of the body can be reduced or related to a tetrahedral form for they are plastic variations of the flat quadrangle” and that even in “many-directional movements a tetrahedral kernel can, nevertheless, be recognised as the simplest expression of the whole tension” (p. 21). This conception may be based on the transformation of the frontal planar net into the tetrahedral net whenever the body twists and so cannot be contained within a single plane (IIIC.33). The four limbs or the four proximal joints can each be conceived at one of the four vertices of the tetrahedral net. Ergonomic researchers have also identified tetrahedral forms within body poses which provide a high degree of structural stability (Dempster, 1955, p. 564).
Since a tetrahedral net can be built by linking the body’s four limbs, or four global joints, it can always be identified within other kinespheric nets. For example, if a body stands on one leg with the other leg reaching dimensionally forward and each arm reaches to the side this pose could be conceived within a higher-order octahedral net or a lower order tetrahedral net (Fig. IIIC-12).

Sequences of locations which have been well learned will be conceptually joined together into map-like images which simultaneously represent an entire spatial environment. A great deal of “cognitive map” research has explored characteristics of these spatial images for environments ranging from small page-sized spaces accessible to eye and arm movements through to large country-sized spaces accessible by traveling. This provides psychological validity for Laban’s use of geometric map-like images of the kinesphere (termed grids, networks, or scaffolding). Similar geometric kinespheric maps have been depicted by artists and architects (eg. Leonardo Da Vinci; Le Corbusier). In the choreutic conception bodily paths and poses are represented as groups of locations within polyhedral-shaped conceptual map-like images of the kinespheric network.